
Six Sigma team members often ask, “How much data do I need to establish the baseline?” for a process that is unstable. There is no valid statistical calculation for sample size in this situation, but that is not much comfort when you are trying to develop a sampling plan in the early stages of your Six Sigma project.
It is possible to apply common sense to the problem and to judge whether the samples taken are likely to give a reliable result for process capability – even to offer a range within which the true value probably lies. Here is how to go about it, including an Excel spreadsheet that can be used as a template for the calculation.
Let’s start with some basic guidelines for gathering a representative sample with special causes. Following these will enable you to avoid some of the most common pitfalls:
- Spread your data collection over as long a period of time as practical (so long as you are satisfied that the measurement system is reliable throughout – remember to be careful with historical data). This will enable you to see as much of the long-term variation as possible. If possible, continue gathering your baseline measurements in parallel with the analyse phase of your project.
- Take account of any known patterns in the process performance – is there a monthly, quarterly or annual cycle? If so, you should make sure that your sampling plan covers the full range of circumstances.
- Does the process suffer occasional, severe problems? If so, you will need to understand their frequency and severity well enough to assess whether the samples taken are typical of the overall process performance. Make sure that you capture a representative mix of these problems along with the day-to-day performance levels.
- Be realistic: if your process has special cause variation, you should expect to need a greater sample size. The sample size formula normally used¹ is based on population sampling. Process sampling is inherently more susceptible to special causes.
How Much Data Is Enough?
The best way to evaluate this is to plot the way the average capability varies as you gather your data (we will call this the cumulative average). This enables you to get at least an intuitive feel for when you have enough data – as the cumulative average flattens out, despite the special causes that may occur from time to time, you start to build some confidence that you have seen ‘enough’ data. If the graph remains unstable or continues to trend up or down, this indicates that the more recent samples are above or below the level you have previously seen, and you need to continue gathering data until the cumulative average has stabilized.
How long should you wait, after the cumulative average has roughly leveled off, before being satisfied that you’ve seen enough? You will need to use your own judgment and knowledge of the behaviour of the process to decide. You might have seen the graph look perfectly level for a month because a problem that crops up every few weeks has not occurred during that time. This would not be sufficient to conclude that you have taken enough data. The best guideline is: If the cumulative average capability seems to be roughly stable over a period when the special causes are fairly representative, you should be safe to conclude your baselining study.
The Excel Tool
The attached Excel spreadsheet makes it easy to look at the cumulative average percent defective. It is based on attribute data because, when dealing with special causes, the simplest way to determine process capability is usually to just count OK and defectives samples. Here are the steps to completing it:
- If you are measuring defects in batches, enter the number of samples in each batch in cell D2 – otherwise, leave it set to 1.
- For each batch (or single unit) that you have checked, enter the date when it was taken in column B and the number of defectives in column C. The graph will continuously update as you enter your data.
- Examine the blue line on the graph (cumulative average percent defective) and ask:
- Has it (more-or-less) leveled off? (You will of course still see some variation, but you should look out for trends or shifts)
- Since when has the blue line been roughly level? We’ll call the time since then the verification period – the time during which our estimated capability does not vary greatly, giving us an indication that we have taken enough samples.
- Are the special causes that the process has experienced during the verification period more or less representative of the typical pattern? (If there are serious but rare special causes that did not occur during this time period, the answer is “no.”)
- If you are satisfied that the blue line has been approximately level over a period when the process has experienced its normal range of special causes, you can use the value given in cell D4, which is the average defect percentage for your whole sample.
- You may be interested (you should be interested) in having some sort of a range on your estimate of the percentage defective. This gives you a feel for how much you can rely on your figure. The spreadsheet can provide this.
- Enter the date from which you believe the cumulative average has been approximately level (the beginning of the verification period) into cell E6.
- The graph will be updated for the verification period with green lines that indicate the range within which the true capability probably lies.
- These lines are not statistically valid confidence intervals – those rely on special causes being absent – so we will refer to the gap between them as the estimate range.
- If the spread between the green lines is too great for your needs, you don’t have enough data. The gap between these lines reduces in approximate proportion to the square root of the sample size – so if you want to halve the gap, you need to quadruple the sample size. You should, of course, expect to have to take more samples when there are special causes present than when there are not.
- For information: The estimate range is calculated by adding the conventional confidence interval to the range of percentage defective estimates seen during the verification period.
Below is a sample graph produced by the Excel spreadsheet. It relates to documentation processing. For each document, the time required to process was measured and a defect was recorded if this exceeded the company’s standard. In the example, the estimated percentage defective is 50.8 percent, and we expect the true value to lie between 45 percent and 58 percent. For a stable process with about 50 percent defectives, we would need about 240 samples to obtain a confidence interval of ± 6.5 percent. Here, we took 360 samples and got an estimate range of ± 6.5 percent. The special cause variation drove the necessary increase in sample size.
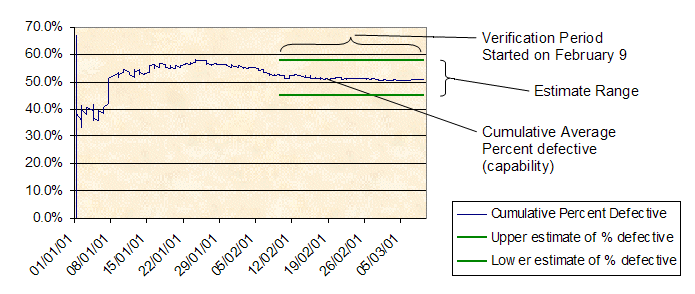
Notes:
1. The formula used to calculate the sample size required for population sampling is n = 4p(1-p)
d²
Where: p is the proportion defective, and d is the maximum error at a 95% confidence level
For example, if you believe that proportion defective is 0.05 and need your estimate to be accurate to within 0.02, your sample size will need to be at least 4 x 0.05 x 0.95 / 0.0004 = 475
Attached Spreadsheet
Download Excel Spreadsheet (1.1 MB)
Download Excel Spreadsheet Compressed (265 KB)