
Three young men, each being infatuated with the same woman, agree to conduct a design of experiment (DOE) of love. Statistics and romance intertwine in this entertaining and educational real-life story. Which bachelor will end up with the young lady’s hand? Will the DOE prove successful?
Peeping into my youthful past, I recall three close friends: Naren, Deepak and me walking to college together every day. I vividly remember one bright sunny morning as we pass a large house with neatly manicured gardens. A young girl rushes out into the greens and abruptly pauses at the sight of three young men passing her gate. Wow! We think she is a vision to behold, fresh as the dew that basks in the early sun and pretty as a rose bud. We freeze in our paths.
Congratulating ourselves on our discovery, we make it a point to pass Renu’s house at that precise hour every day (Naren’s fantastic information network has already discovered her name.) Sure enough, she is there day after day. We float by in a trance, weak kneed, ogling at her, and excitedly discuss her after our class.
One day it finally happens. Renu gives us a dazzling smile and winks at us. The three Romeos are floored and stupefied. This can’t be true. Did we imagine it? It was too far fetched for all three of us to have imagined the same thing. Our hearts turn a summersault. Eager for more, we pause expectantly by her house the next day and lo, there comes the smile and the wink. We are now positively starry eyed, and almost dance our way to college.
Strangely, Deepak looks rather thoughtful. “Come on man, let’s celebrate! She did it again” I try to cheer him into the general loony mood. “Really?”, he retorts, “But there is a little catch. Who did she wink at? You, me or Naren?” I wake up with a start. Now, this is serious. I too wear his brooding cap. Naren looks up and joins the gloom. “Certainly, she couldn’t be winking at all three of us?” We don’t bother to reply.
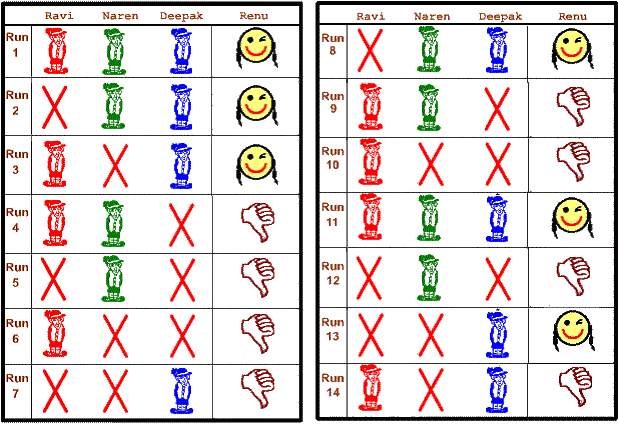
The smile and the wink fail to cheer us the next day. “Let’s ask her up front” I put in my two cents. They seem to agree, but the question of who will win her attention still remains. We must find out which one of us Renu fancies. Thinking hard, slowly but surely a game plan evolves. We decide to find out through planned experimentation. Instead of all three of us walking together, we decide to go past her house in a well-planned pattern of twos and singles. We quickly put our plan into action. We already know Renu’s response to all three of us walking together and tabulate it as below:

The next day, I stay back. Deepak and Naren walk together past her house. Much to my dismay, the smile and wink greet them enthusiastically. We tabulate this result as:

It’s now Naren’s turn to stay back. Deepak and I dutifully get the smile and wink. Prompt in our paperwork, we put down these results too.

The data is building up, and we are all set to jump to wishful conclusions. We tell Deepak that she’s just playing games, and keep him back at home. Naren and I take a confident walk, eager to prove our theory of Renu playing games, but are in for a shock. Renu simply does not make an appearance. Less sure about ourselves, we tabulate this result too.

Deepak gives the laugh that love struck boys usually give, and suggests that we now walk one person at a time. Naren and I do our part and encounter Renu’s vanishing trick. Results are dutifully tabulated.

Deepak is on cloud nine by now. He puts on his best shirt, shines his shoes, and walks past Renu’s house, chin up. He actually walks up and down a couple of times, but Renu still fails to appear. Naren and I take pleasure in tabulating this result.

Deepak by now looks like a deflated balloon, and Naren and I are frankly perplexed. “What’s the meaning of this? Is she trying to twist us around her little finger?” Deepak is rightly antagonized. “Look, rather than jumping to conclusions, let’s run this combination of experiments again. At the end of all the runs, we can analyze the data and form some hypothesis.” My statistics classes have started showing their effect. My friends agree to the suggestion.
“I am not going on a Friday” Naren states with a sudden urge to cling to superstitions. The order in which the runs are carried out is decided by rolling a pair of dice and the matter is settled. Over the next week, we carry out the experiment again and the results are put together. We are now ready for the judgment. We consolidate the results from both the sets of runs as follows:
We decide to analyze the results by the change in Renu’s response to the presence or absence of each of the Casanovas. Results (I discovered later that they are called effect plots in DOE parlance) showed as follows.
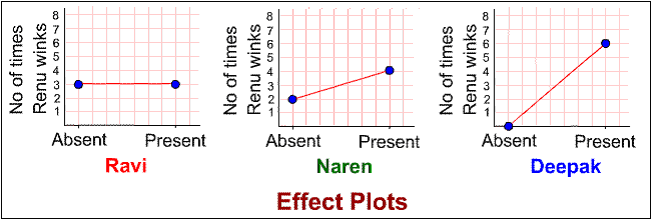
Obviously, Deepak is the clear winner. Naren and I shake Deepak’s hand, wish him good luck and go on to chase the other damsels in the neighborhood. Not until much later, when I studied statistics and DOE, did I realize that we had performed a Factorial Experiment as we pursued Renu.
There were three Factors in this experiment: Naren, Ravi and Deepak. A factor is an independent variable in an experiment whose state can be varied. In a planned experiment, the factors are deliberately varied in a predetermined manner. The response is measured at every run of each combination. In a scientific experiment, pressure and temperature of the reaction could be two of the factors. These are varied across the experimental pattern and the response characteristic (e.g., yield of the reaction) is measured.
Each factor was evaluated at two Levels: the person was Present or Absent. A level is a state of the factor that is deliberately varied. Experimentation is typically done at two, or occasionally three levels for every factor. Combining all factors and their levels can become too large and daunting a task if every factor is changed one at a time. An efficient experimental design that varies multiple factors at the same time can reduce the number of runs to a great extent, still providing enough information for confident results. Levels can be discrete like the Present / Absent levels that our experiment had, or can be numeric, such as 80 degrees / 100 degrees centigrade for the temperature factor in a chemical reaction.
The objective variable that is calculated is the Response, which measures:
- The relationship between the change in level of each of the factors and the change in response.
- The change in response for a change in each factor level (sensitivity)
In our experiment, the Response was attribute data expressed as whether Renu winked or not. We could gage the size of the response by counting favorable responses to each factor at each level. The Response can also be variable data, such as a change in purity from 90 percent to 95 percent, where the numerical value of the response is averaged for each level. The difference in response is called the Effect, and is expressed using an effects plot as shown above.
The experiment we conducted was Balanced since each factor at each level was evaluated at an equal number of other factor-level combinations. A balanced experiment gives the same evaluation advantage to each factor and helps remove bias that may appear as a result of an unequal amount of data for each factor-level combination.
Randomization was achieved by rolling the dice to determine the sequence of runs. This is important since it gives all external factors an equal chance to affect every run of the experiment. A non-randomized experiment stands a great risk of external factors acting in a systematic manner, adding noise to the response.
Conducting two sets of experimental runs led to Replication, providing more data and greater confidence in evaluating the results. One drawback to conducting more replications is the potential for added costs in the experimentation process.
What then went wrong in run 7 and run 14? Why didn’t Renu respond to Deepak’s presence?
In the first case (run 7), it was a Lurking Variable that played a role. Renu happened to have a father who was built like a Gorilla and had a very foul temper. On the day Deepak went alone in the first Replication, the father had confined Renu to her room for some trivial reason. A lurking variable like Renu’s father is an external factor that strikes suddenly and randomly to affect the response and confuse the results. In the second case (run 14), it was Renu herself who was in a foul mood and refused to perform as expected. After all she was human, and couldn’t be expected to fall in line with statistics all the time. This represents an Experimental Error commonly encountered in experimentation.
I was lucky to learn structured Design of Experiments early in life!
In case you’re wondering what happened to the three Romeos…
Deepak married Renu, and went ahead to become a software professional. Deepak and Renu live in Boston.
Naren is a research scientist with a world-class pharmaceutical company in Philadelphia. Early training in Experimental Design undoubtedly prepared him for a great scientific career.
Ravi is the Managing Director of Symphony Technologies Pvt. Ltd.