One of the most difficult topics for those learning how to use statistics is hypothesis testing. Solving a number of examples will help convince potential and new Six Sigma practitioners of the importance of the concepts behind this tool. However, the necessary steps and their formulation take some additional effort. An appropriately designed solution template for this purpose can ease the difficulties of the learning process.

Suppose that we want to decide whether the mean (m) of the population under consideration exceeds, does not exceed or differs from a given value (m₀). To make that decision, we take a random sample, compute the mean (), and then apply a statistical inference technique called hypothesis testing. First, we describe the hypothesis tests for one-population mean. The results from this exercise will translate to other hypothesis-test analogies of the one-sample z-interval and one-sample t-interval confidence-interval procedures, respectively. The third is a nonparametric method called Wilcoxon signed-rank test, which applies when the variable under consideration has a symmetric distribution. For other hypothesis tests beyond the tests for one-population mean, the formulas for test statistics (Z) will be used in Step 3 instead of test statistics:

Hypothesis Tests for One-population Mean

We will solve the following hypothesis tests for a one-population problem using the template to be designed. The solution text will appear as underlined or as a choice to be selected or deleted, appropriately.

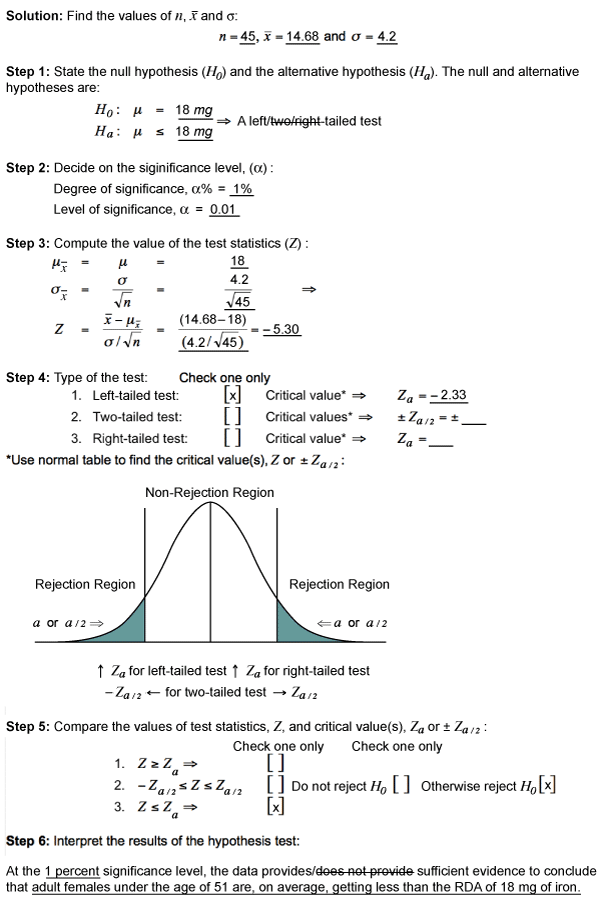
Example: The Food and Nutrition Board of the National Academy of Sciences states that the recommended daily allowance (RDA) of iron for adult females under the age of 51 is 18 milligrams (mg). A sample of iron intake in was obtained during a 24-hour period from 45 randomly selected adult females under the age of 51. It revealed that the sample mean () was 14.68 mg. At the 1 percent significance level, does the data suggest that adult females under the age of 51 are, on average, getting less than the RDA of 18 mg of iron? Assume that the population standard deviation is 4.2 mg.

P-Value Approach to Hypothesis Testing

This can also be modified to examine a second approach to hypothesis testing, the p-value approach with a minor modification. The p-value (also known as the observed significance level or the probability value) indicates how likely or unlikely observation of the valueobtained for the test statistics wouldbe if the null hypothesis (H₀) is true. In particular, a small p-value (close to 0) indicates that observation of the value obtained for the test statistics would be unlikely if the null hypothesis (H₀) is true. Accordingly, Steps 4 and 5 will be modified as follows for the p-value approach. For a two-tailed test, as required, the amount a of will be halved in the alterative Steps 4 and 5.

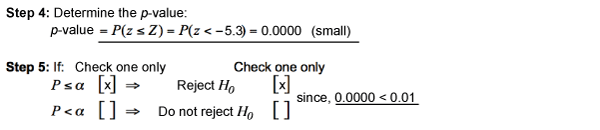
Conclusion: Help for New Black Belts

The solving of a problem using these steps will draw the attention of new Black Belts to the important aspects of the concepts. Following this solution template, they will find it easier to solve difficult hypothesis testing questions.

Note: The author acknowledges the work of Neil A. Weiss in his book Introductory Statistics (Pearson Education Inc., 2005).