
The purpose of doing linear regression is to predict the effect of some input variables on an output variable. But sometimes the input variables are correlated with each other. When that happens, it reduces the value of the prediction. Let’s explore this in greater depth.
Overview: What is the variance inflation factor (VIF)?
When doing a multiple regression analysis, you want to be able to predict the effect your independent variables have on your response or dependent variable. The degree of correlation between your independent variables is an important consideration. This between-variable correlation is called multicollinearity. VIF is the measure of the degree of multicollinearity.
If there is multicollinearity in your regression, the variance of your predictor variables will be increased or inflated. This increased variance will affect the coefficients of the predictor variable in your prediction equation. In other words, multicollinearity misleadingly inflates the standard errors, therefore making some variables statistically insignificant when they should be significant.
The formula for VIF is:
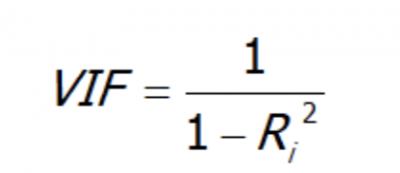
The term R squared is the coefficient of determination, which represents the proportion of the variation in the dependent or response variable that is explained by the independent variable(s).
For example, a VIF of 1.8 tells you that the variance of a specific coefficient is 80% bigger than what you would expect if there was no multicollinearity. This is calculated by regressing each independent variable against the other variables.
The rules of thumb for determining whether your VIF is a concern are:
- 1 = not correlated
- Between 1 and 5 = moderately correlated
- Greater than 5 = highly correlated
Most statistical software displays the VIF in the regression output. In the example below, note the high VIF values for speed and thickness. One of them can be eliminated in the final regression equation since they are highly correlated.
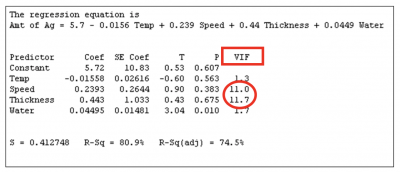
If your VIF is high and there is high multicollinearity between two variables, you don’t need both of them in your equation.
Here are the strategies for deciding which value to eliminate:
- Start with the factors that you can control. In the example above you can control speed better than thickness, so eliminate thickness
- Eliminate highest VIF value – again thickness has a higher VIF at 11.7.
- Eliminate the least significant factor, that is, the factor with the highest p value or lowest t value. Looks like thickness is the one to go.
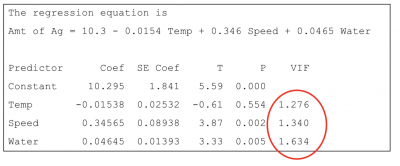
Below is the final output and regression equation once thickness was removed and the final regression model run. You will see the values of VIF are now very low and multicollinearity has been eliminated.
An industry example of the variance inflation factor
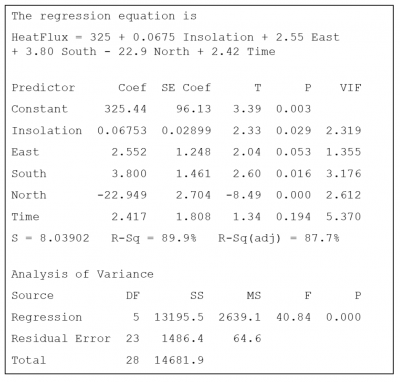
As part of a test of solar thermal energy, a large utility company wanted to measure the total heat flux from the homes in their service area. Heat flux can be predicted by insolation (a measure of solar radiation energy received on a given surface area in a given time), by the position of the focal points in the east, south, and north directions, and by the time of day.
Below is the computer output for their first run regression analysis. The VIF values show there is no problem with multicollinearity. They can now continue doing their analysis.
Frequently Asked Questions (FAQ) about the variance inflation factor
What does the variance inflation factor measure?
It is a measure of the degree of multicollinearity or correlation between the independent variables in your multiple linear regression analysis.
What is the effect of high multicollinearity?
The variance, or standard errors, of the independent variables will be inflated, which may provide false information about the significance of the factors in your regression equation.
What do I do if I have a high variance inflation factor?
If you have a high variance inflation factor, it means some of your independent variables are correlated. Since they both provide the same information, you can eliminate one of them. You can make a decision on which one to eliminate based on the degree of control you have on the variable, or choose the one with the highest p value or t value.