In order to prove that a process has been improved, you must measure the process capability before and after improvements are implemented. This allows you to quantify the process improvement (e.g., defect reduction or productivity increase) and translate the effects into an estimated financial result – something business leaders can understand and appreciate. If data is not readily available for the process, how many members of the population should be selected to ensure that the population is properly represented? If data has been collected, how do you determine if you have enough data?

Determining sample size is a very important issue because samples that are too large may waste time, resources and money, while samples that are too small may lead to inaccurate results. In many cases, we can easily determine the minimum sample size needed to estimate a process parameter, such as the population mean .

When sample data is collected and the sample mean 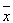is calculated, that sample mean is typically different from the population mean 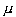. This difference between the sample and population means can be thought of as an error. The margin of error 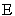is the maximum difference between the observed sample mean 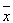and the true value of the population mean :

where:

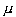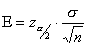
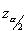is known as the critical value, the positive 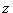value that is at the vertical boundary for the area of 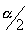in the right tail of the standard normal distribution.

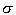is the population standard deviation.

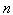is the sample size.

Rearranging this formula, we can solve for the sample size necessary to produce results accurate to a specified confidence and margin of error.

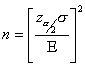
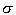This formula can be used when you know and want to determine the sample size necessary to establish, with a confidence of 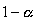, the mean value 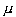to within 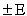. You can still use this formula if you don’t know your population standard deviation 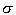and you have a small sample size. Although it’s unlikely that you know 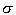when the population mean is not known, you may be able to determine 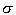from a similar process or from a pilot test/simulation.

Let’s put all this statistical mumbo-jumbo to work. Take for example that we would like to start an Internet service provider (ISP) and need to estimate the average Internet usage of households in one week for our business plan and model.

Sample Size Calculation Example

Problem
We would like to start an ISP and need to estimate the average Internet usage of households in one week for our business plan and model. How many households must we randomly select to be 95 percent sure that the sample mean is within 1 minute of the population mean 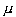. Assume that a previous survey of household usage has shown 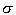= 6.95 minutes.

Solution
We are solving for the sample size .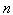

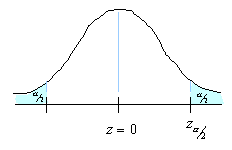
A 95% degree confidence corresponds to 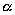= 0.05. Each of the shaded tails in the following figure has an area of 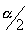= 0.025. The region to the left of 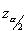and to the right of 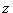= 0 is 0.5 – 0.025, or 0.475. In the table of the standard normal (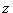) distribution, an area of 0.475 corresponds to a 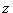value of 1.96. The critical value is therefore 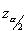= 1.96.

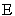The margin of error = 1 and the standard deviation 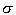= 6.95. Using the formula for sample size, we can calculate :

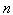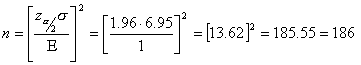
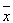So we will need to sample at least 186 (rounded up) randomly selected households. With this sample we will be 95 percent confident that the sample mean will be within 1 minute of the true population of Internet usage.

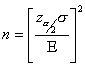
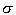This formula can be used when you know and want to determine the sample size necessary to establish, with a confidence of 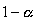, the mean value 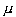to within 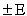. You can still use this formula if you don’t know your population standard deviation 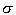and you have a small sample size. Although it is unlikely that you know 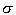when the population mean is not known, you may be able to determine 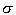from a similar process or from a pilot test/simulation.