While there are many definitions of resolution, we are interested in how it applies to data and the amount of information we can see and learn from. We will explore resolution in the context of doing Measurement System Analysis (MSA) and Design of Experiments (DOE), with the emphasis on DOE. 

Let’s examine what resolution is, some of the benefits of having high resolution, and how it impacts on your understanding of data analysis.

Overview: What is resolution? 

When we speak of resolution in terms of Measurement System Analysis (MSA), it refers to the resolution or discrimination of the measurement system. 

If your analysis is using a ruler to measure the length of product, requires measurement units in terms of one-quarter inches, but can only measure in units of inches, your measurement system has low resolution.

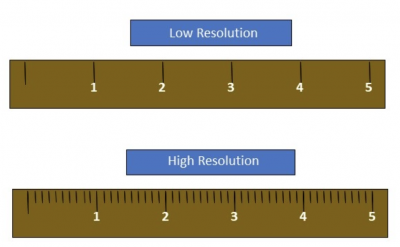
If the scale in your testing lab needs to weigh your product in increments of plus and minus 1 gram but can only weigh in increments of plus and minus 5 grams, then your measurement system has low resolution. 

There will always be a tradeoff between cost and incremental resolution. You will typically seek a higher resolution than you need to assure you have sufficient resolution to see what you need in your measurements.

Resolution in DOE refers to the degree of confounding or aliasing that occurs in a fractional factorial design. 

A full factorial DOE design explores every possible combination of factors, including interactions. It provides a complete understanding of the relationship between the factors. For example, a full factorial design with three factors (A, B, and C) would provide information on the main effects of A, B, and C. It would also provide two way interactions for AB, AC, and BC, along with a three-way interaction of ABC. This would be defined as full resolution since you can independently know the impact of all individual main effects and interactions on the response variable.

When you conduct a fractional DOE, you use a subset of the full design. This results in a loss of information. Confounding or aliasing means you can no longer know the independent impact of your main effects and interactions on the response since they will be confounded with other main effects and interactions. 

Let’s say we have five variables: A, B, C, D, and E. In a two-level full factorial DOE, you would need 2^5 = 32 runs. But, we could choose to do a half fraction, or 16 runs, or even a quarter fraction, or 8 runs. Anything less than the full factorial will result in some level of confounding.

The degree of resolution is expressed in Roman numeral values starting with III. Here are some of the more common definitions of resolution values:

1. Resolution III: Main effect may be confounded with a 2-way interaction. Used for screening experiments.
2. Resolution IV: 2-way interactions may be confounded with each other. Main effects are not confounded with 2-way interactions but may be with a 3-way interaction.
3. Resolution V: 2-way interactions are confounded with 3-way interactions. Main effect is confounded with 4-way interactions.
4. Resolution VI: 3-way interactions are confounded with each other. 2-way interactions are confounded with 4-way interactions. Main effect may be confounded with a 5-way interaction.

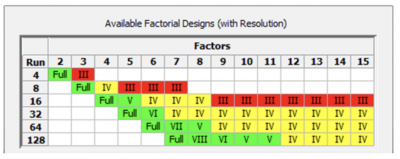
Minitab software provides a table showing the number of factors and number of runs for different fractions. It also shows the resolution level. Green represents high resolution, yellow medium resolution, and red is low resolution, where your main effect is confounded with your two-way interactions. 

Let’s assume we have a two-level, 5-factor experiment (32 runs) that we run as a half fraction (16 runs). 

Note the table shows a V resolution for 5 factors and 16 runs.

Most statistical software will produce an aliasing table showing the confounding and resolution. 

Here is what it looks like for our 5-factor example if we run a half fraction experiment:

This can be interpreted as main effects are confounded only with 4-way interactions, and there are no 2-way interactions confounded with other 2-way interactions. 

Although your main effects are confounded with 4-way interactions, and 2-way interactions are confounded with 3-way interactions, you can be pretty confident that you can determine the impact of your main effects and 2-way interactions on your response variable. That is why the V resolution in the table above is green.

Here is a fun way to understand resolution and confounding using your fingers.

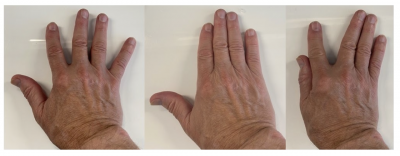
Using our V resolution (total number of fingers) you can see that the thumb (main effects) is confounded with some 4-way interactions, and some 2-way interactions are confounded with some 3-way interactions. The alias table shows which ones are confounded.

3 benefits of resolution 

There are no benefits to resolution. Full resolution is your best condition. But, the information provided by knowing your resolution has benefits for your decision-making process. 

1. Describes the confounding of your interactions 

Confounding, also known as aliasing, occurs in fractional factorial designs because the design does not include all of the combinations of factor levels. 

For example, if factor A is confounded with the 3-way interaction BCD, then the estimated effect for A is the sum of the effect of A and the effect of BCD. You cannot determine whether a significant effect is because of A, because of BCD, or because of a combination of both. 

A low resolution will indicate significant confounding between your main effects and lower-order interactions. High resolution gives you confidence you can discriminate between the impact of your main effects and lower-order interactions while ignoring confounding of higher-order interactions. 

2. Save time and money

If you select an acceptable level of resolution and use a fractional factorial DOE design, you will save time and money over doing a full factorial. 

3. Understand what information you give up by doing a fractional factorial 

A fractional factorial design, by definition, will result in a reduced amount of information about how your factors impact your response variable. Your degree of resolution will indicate how much and where you lose the information. 

Why is resolution important to understand? 

The degree of resolution of your DOE design will help you understand the value of your experiment. 

Knowing your confounding or alias structure 

Understanding your experimental resolution will help you evaluate whether your experiment is sufficiently powerful to provide the information you need for decision-making. Your resolution provides the resulting confounding of your main effects and interactions.

Helps select the appropriate fraction for your design 

There will be a tradeoff between the number of runs in your experiment and the amount of information you lose due to confounding. Your choice of desired resolution will help you balance runs and confounding. 

Keep in mind what’s important 

Higher-order interactions are usually less important than lower-order ones. In other words, you should be more concerned about the confounding of 2-way interactions than 4-way ones. You can impact that by the selection of your resolution.

An industry example of resolution

Coming out of the Analyze phase of a DMAIC project, the improvement team identified seven possible factors that could impact the quality of the company’s product. Although they did a multiple linear regression to narrow down the factors, they were not able to identify the interactions or confounding between factors. 

The team’s Master Black Belt suggested they do a screening Resolution III DOE to statistically confirm the factors. This would require an experiment of 8 runs instead of the 128 for a full factorial design. 

Although there was some confounding between the main effects and some 2-way interactions, they were confident that 4 of the 7 factors were good candidates for a future DOE. 

They had the option of running a half fraction with 8 runs, or a full factorial with 16 runs. Using a half fraction would be a IV resolution. Although the main effects were only confounded with 3-way interactions, they were concerned the 2-way interactions were confounded with each other. They believed there were some significant 2-ways that could be important, so they chose to do the full factorial where resolution was not an issue. 

Three of the four factors were determined to be significant, as well as some of the 2-way interactions. This served as the model for the process and was used to predict the response variable at different settings for the factors.

3 best practices when thinking about resolution

Here are a few tips on selecting and interpreting resolution and confounding. 

1. Select your desired resolution before you run your fractional factorial experiment 

Once you have identified the potential factors to be included in your experiment, you can choose the fraction you want to run. This will be dictated by your desired resolution. 

2. Screening experiments 

If you have a large number of potential factors to explore, you will want to use a low level resolution like III to screen out and narrow down the potential factors. 

3. Don’t worry too much about higher-order confounding 

Most of the world is governed by the impact of main effects and 2-way interactions. Three-way interactions and above are difficult to understand, so the odds of them having a significant impact on your response variable is minimal. 

If your main effects and 2-way interactions are confounded with 3-way, 4-way, or more interactions, don’t worry too much about it. 

Frequently Asked Questions (FAQ) about resolution

1. What is the resolution for a half fraction with 4 factors? 

It is a resolution IV. This means the main effects are confounded with some 3-way interactions, and some of the 2-way interactions are confounded with some other 2-way interactions. 

Below, you see how you can use the finger approach to illustrate confounding.

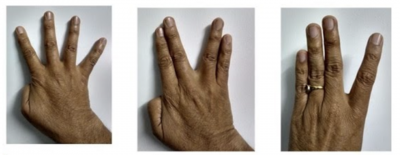
Image source: Resolution IV using your fingers

2. What does DOE resolution tell you? 

The resolution in a fractional factorial DOE shows the confounding or aliasing between the factors and interactions. 

3. What can I use a resolution III design for? 

The lowest-level resolution is III. This is when your main effects are not confounded with other main effects but are confounded with 2-way interactions. This design is useful as a screening experiment to reduce the number of potential factors.

Resolution wrapup

Resolution becomes important when talking about fractional factorial DOE experiments. It describes what factors and interactions are confounded with each other. Confounding will make it more difficult to attribute the impact on your response variable. High-resolution designs allow you to understand the impact on your response variable due to main effects and lower order interactions. A low-resolution design will mask the impact and make it difficult to distinguish where the effect is coming from.