The gage R&R study is the standard tool in the Six Sigma process improvement methodology to evaluate the adequacy of a measurement system with regard to measurement variability. While it is well established and widely used in the discrete manufacturing industry, it is less useful in process industries where the nature of measurements is different, necessitating a different approach to the assessment of measurement systems in these industries.

A measurement system, as defined in a gage R&R, consists of a number of operators using a number of gages to measure parts in accordance with some defined procedure. A gage R&R partitions the total measurement variation into the following categories:

1. Gage-to-gage
2. Operator-to-operator
3. Replicate-to-replicate
4. Part-to-part

The first three categories of variation comprise noise (i.e., undesirable measurement variation), while the fourth category of variation is the quantity that needs to be determined accurately. In general, the desire is that the part-to-part variation is large relative to the sum of the other three categories of variation so a Six Sigma practitioner can be confident of discerning the true part-to-part variation without being swamped by the measurement noise.

The gage R&R thus enables the analyst to assess the ability of the measurement system to discern a within-specification part from an out-of-specification one and to take the appropriate corrective action when necessary. It is the appropriate tool to use when the measurement system is employed in inspecting discrete parts off a production line for conformance to specifications.

Gage R&R Premise Not Applicable

In process industries, however, the premise on which the gage R&R is based is not applicable to the many gages that are employed to perform on-line measurements. A typical example from the mining industry would be the belt scale – a gage mounted under a conveyor belt to measure the mass flow (tons per hour) of material being processed. The scale is an automated device producing a continuous measurement that is sampled by a computer. There is typically only one scale at each measurement point in the system and no operator involvement is required to produce a measurement. As a result, gage-to-gage and operator-to-operator variations are non-issues, making it unnecessary to partition the total variation into its various components as with a conventional gage R&R.

In the case of an on-line measurement, analysts are interested in two questions:

1. With the measured value of a physical quantity by the gage, what is an estimate of the true value?
2. What is an estimate of the uncertainty or confidence interval around the estimated true value?

In order to answer these two questions, the total measurement error of the gage needs to be partitioned into its systematic and random components. Mathematically, the systematic-error component is characterized by a deterministic function while the random-error component is characterized by its variance. The former enables the analyst to estimate the true value from the measured value while the latter allows the establishment of a confidence interval around this estimated true value.

For analysis, an on-line gage may be conceptualized as a measurement process, which takes the true value, X_T, of a physical quantity as its input and produces a measured value, X_M, as its output (Figure 1). The statistical model for this measurement process may be written as: 

X_M = X_T + f(X_T) + e or X_M – X_T = f(X_T) + e

Where: X_M = measured value of physical quantity
X_T = true value of physical quantity
f(X_T) = systematic-error function
e = random measurement error

Perfect Gage / Real Gage

The random error, e, is assumed to be normallydistributed with a mean and variance of zero and s², respectively. It is further assumed that the distribution is invariant with respect to X_T. A perfect gage will have no systematic or random error (i.e., f(X_T) = 0 = e), and the measurement process reduces to X_M = X_T. A real gage, however, will have f(X_T) ¹ 0, e ¹ 0 and consequently, f(X_T) and s² will have to be determined by calibration. The gage is calibrated by taking N measurements, over the range of interest, of the physical quantity where the true value, X_T, is known independently, thereby producing a set of N paired data points of X_T and X_M. 

If the mathematical form of the error function f(X_T) is known, it is then a relatively straightforward matter to perform a regression analysis on the calibration data to estimatethe parameters of the function. The variance of the random error may then be estimated by computing the mean-squared value of the residuals of (X_M – X_T) around the fitted error function. However, this estimate of s² is accurate only if the error function f(X_T) has been correctly selected. 

Some care should be exercised in selecting the form of the error function f(X_T) as the choice will have a critical effect on the quality of both the systematic and random-error estimates.There is a natural tendency to gravitate toward a linear equation (i.e., f(X_T) = A * X_T + B), for simplicity but this should be resisted. The form of f(X_T) will, in general, depend on the nature of the gageas well as the specific cause of the error and it is unwise to automatically assume that all gages are linear with respect to their systematic error.

If no a prori knowledge of the gageis available to indicate the nature of the error function then an iterative procedurewill be required to make that determination (Figure 2). To begin, an initial guess as to the form of f(X_T) is made based on a visual inspection of the scatter plot of (X_M – X_T) versus X_T. A regression analysis can then be performed with this provisional f(X_T) and the residuals checked for randomness and normality using residual and normal-probability plots, respectively. If the function has been chosen correctly, the residual plot of (X_M – X_T) – f(X_T) versus X_T should be random and structureless while the normal-probability plot of (X_M – X_T) – f(X_T) should show an approximate straight line indicating a normal distribution. 

Failing Randomness or Normality Inspection

Should the residuals fail either the randomness and/or the normality inspection, the selected error function is not a good fit for the data. A new function must then be selected and the process repeated until the residuals satisfy both the randomness and normality conditions. At this point, the error function is a good fit and the random error can then be estimated by computing s² from the residuals.

To illustrate the preceding discussion, consider a hypothetical gage calibration with the scatter plot of (X_M – X_T) against X_T shown in Figure 3. A visual inspection of the data indicates that the function f(X_T) is probably non-linear in nature. However, if one persists in fitting a linear equation to the data, then one obtains the regression,residual and normal-probability plots shown in Figures 4, 5 and 6, respectively. The residual plot, Figure 5, clearly shows a non-randomstructure while the normal-probability plot, Figure 6, indicates a strongdeparture from normality. These observations indicate that,in this case, the validity of the linear equation as the error function is strongly suspect.

Returning to the function-selection step of the process, we try again with a quadratic function to account for the curvature in the data. The corresponding regression, residual and normal-probability plots are shown in Figures 7, 8 and 9, respectively.

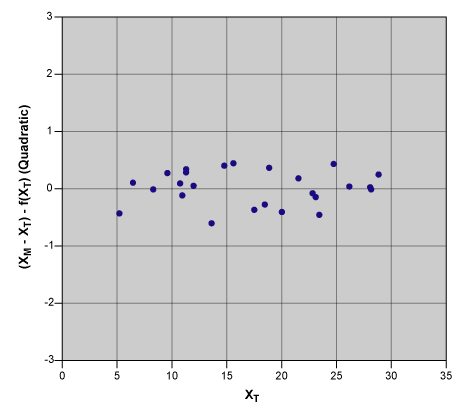
Visually, the quadratic function fits the data much better here than in the linear case (Figure 4). The residual plot displays a random scatter of points about the (X_M – X_T) – f(X_T) = 0 line with no discernable structure and the normal-probability plot is approximately linear, indicating a normal distribution for the residuals. Hence, it can be concluded that the quadratic function is a reasonable representation of the gage systematic error. The final step in the measurement systems analysis (MSA) is to compute an estimate of the random-error variance, s², from the mean-squared value of the residuals. The MSA result can then be stated as: 

Systematic error function: X_M – X_T = -0.0141X_T² + 0.3122X_T – 0.8857
Random error variance: s² = 0.1015 =>s = 0.3186

How is this result utilized? As an example, suppose that the gage has produced a measured value of X_M = 25.70. To correct for the systematic error, we substitute X_M = 25.70 into the error function and solve for the true value, obtaining X_T = 29.81. A 3 sigma confidence interval around X_T is then given by X_T = 29.81 ± 3s = 29.81 ± 0.956. The process MSA thus enables one to determine the true value from the measuredvalue together with an estimate of the uncertainty around X_T. 

More Considerations for Process MSA

Some additional mathematical and practical considerations in conducting a process MSA: 

1. The function selected to represent the systematic error should be sparse. This means that it should contain as many parameters as necessary to represent the data well, but no more. It is tempting to add more parameters to get a better fit to the data but it also is bad practice to use a function that is more complex than necessary.
2. If the error function contains p parameters, then the number of calibration data points should be at least N = p + 1 to afford a sufficient number of degrees of freedom to estimate all the parameters as well as s². This, however, is only the absolute minimum number of data points required. A greater number is always better from the statistical standpoint, but this has to be balanced against the time, effort and resources required to obtain the data.
3. The calibration data points should be approximately evenly spread throughout the measurement range of interest. It is undesirable to have data points clustered together at some sections of the measurement range and gaps with no data in others.
4. The error function should not be extrapolated beyond the calibration-data range unless there is good reason to believe that its validity extends to those regions.
5. The parameters of the error function will themselves have uncertainties associated with their estimated values. The estimation of these parameter uncertainties is beyond the scope of this article but those interested may consult any standard statistics text for more information.
6. Assessing the merit of an error function solely through its regression coefficient, R², is inadvisable. R² is the fraction of the total variation that is accounted for by the function and all else being equal, a higher R² indicates a better fit of the function to the data. However, all else may not necessarily be equal when comparing different functions. R² naturally increases with the number of parameters in any given function. So, when comparing a higher-order polynomial with a lower-order one, then it is a given that the former will have a higher R², but it does not necessarily follow that it represents the data any better in the practical sense. The higher-order polynomial may merely be tracking the noise in the data. However, when comparing different types of functions such as log, trigonometric and polynomial with the same number of parameters, then their R² values are a useful indicator of their respective “goodness of fit.” In any case, R² should always be used in conjunction with a visual inspection of the regression plot in assessing how well a prospective error function fits the data.
7. The Anderson-Darling hypothesis test can be used in conjunction with the normal-probability plot to provide a more objective assessment of the normality of the residuals. 

A process MSA is essentially a special case of a single-factorexperiment in which a model equation for the relative output of the process, (X_M – X_T), in relation to its input (X_T) is trying to be established. All the usual precautions of normal experimentation, such as randomization, apply here as well. The MSA is as much an art as a science and requires no small degreeof skill and judgment as well as a combination of mathematical,technical and practical knowledge to execute well.

The author acknowledges the work of D.C. Montgomery and G.C. Runger in their book Applied Statistics and Probability for Engineers and the National Institute of Science and Technology’s e-Handbook of Statistical Methods.