
Before I started my Six Sigma journey, I thought that having more samples was always better. But when I learned about sample size calculation and selection and their practical importance, I became more conscious of the samples that one should take – that is, I should take the right sample size, not necessarily the biggest sample size.
If we take more samples, then the sample statistics that we get will be closer to the actual population statistics. This means that the analysis that we will do is a better representation of the actual at a certain level of confidence. Depending on the difference between a point of reference and an evaluation or the difference between groups of evaluations, as well as the identified risks (alpha and beta), the sample size requirement will vary. Having an incorrect sample size will lead to decision errors – we will not have enough evidence to prove our claim with the number of samples we collected.
Challenges with Too Few or Too Many Samples
Say we collect 30 parts to test whether a particular machine setting affects a parametric measurement, but based on the sample size calculation we need at least 50 parts. If we collect the results and run a hypothesis test, there is a possibility that we may not detect the difference or expected change that we want to. We may have to re-run additional samples, which will take us even longer.
In contrast, if we collected 50 parts to evaluate the effectiveness or impact of the change but the requirement is calculated to be only 30 parts, there are also consequences tied up. Having more samples will require more resources – such as longer evaluation time and higher cost – while having the right sample size will make the evaluation faster and more economic, leading to optimization. Furthermore, if I run a hypothesis test, there is a possibility that we will detect a smaller difference, which may result in a statistically significant difference generated by your software but that has no practical significance.
If you have a pass/fail criterion that you want to use to evaluate your process, this will require you to use much larger samples compared to a continuous metric, which will be, therefore, more expensive.
As shown in Figure 2 below, the critical difference will have a critical impact on the decision whether a change should be accepted or not.
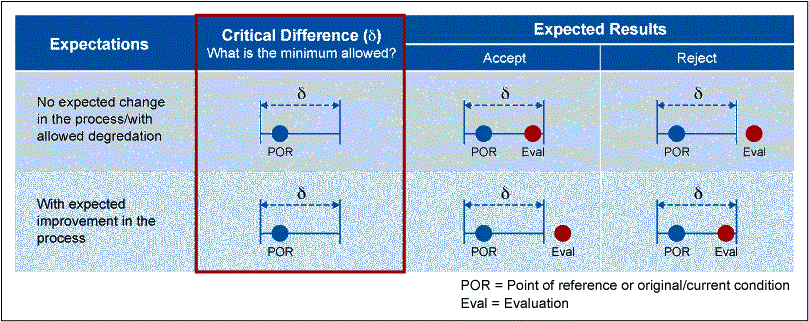
If an incorrect critical difference is established, an inappropriate sample size will be collected and the analysis will be referred to this wrong sample size. Deciding on the result of the evaluation using an inappropriate sample size will lead to risks that will affect your operations and your customers. The table below shows when you should proceed with changes based on the critical difference.
| Expectations vs. Results with Critical Difference Identified | |||
| Expectations | Judgment | Sample Size Calculated Based on Critical Difference Identified | |
| Correct | Incorrect | ||
| No expected change in the process/with allowable degradation | Not significant | Proceed with the change | Consumer risk (recalculate sample size and rerun evaluation) |
| Significant | Do not proceed with the change | Producer risk (recalculate sample size and rerun evaluation) | |
| With expected improvement/gain in the process | Not significant | Do not proceed with the change | Producer risk (recalculate sample size and rerun evaluation) |
| Significant | Proceed with the change | Consumer risk (recalculate sample size and rerun evaluation) | |
Summary
The right sample size is needed to:
- Successfully detect the change expected from a process change.
- Use resources properly during the evaluation process.
- Avoid decision errors that may affect the operations and customers based on the process change.
Always weigh the trade-off between practical and statistical significance.