In some situations, Six Sigma practitioners find a Y that is discrete and Xs that are continuous. How can a regression equation be developed in these cases? Black Belt training indicated that the correct technique is something called logistic regression but this tool is often not well understood. An example about a well-known space shuttle accident can help to demystify logistic regression using the simplest logistic regression – binary logistic regression, where the Y has just two potential outcomes (i.e., “yes” or “no,” or 0 or 1).

The data in Table 1 comes from the Presidential Commission on the Space Shuttle Challenger Accident (1986). The data consists of the number of the flight, the air temperature at the time of the launch and whether or not there was damage to the booster rocket field joints (no = 0, yes = 1).

Table 1: Data from Shuttle Investigation
Flight	Temp.	Damage		Flight	Temp.	Damage
STS 1	66	0		STS 51A	67	0
STS 2	70	1		STS 51C	53	1
STS 3	69	0		STS 51D	67	0
STS 5	68	0		STS 51B	75	0
STS 6	67	0		STS 51G	70	0
STS 7	72	0		STS 51F	81	0
STS 8	73	0		STS 51I	76	0
STS 9	70	0		STS 51J	79	0
STS 41B	57	1		STS 61A	75	1
STS 41C	63	1		STS 61B	76	0
STS 41D	70	1		STS 61C	58	1

Using normal regression and given a particular temperature at launch time, this data can be used to calculate the probability of damage to the booster rocket field joints.

There are five steps to apply logistics regression.

Step 1. Graphically Visualize the Data

A stratified dot plot can be used to graphically display the data. It is obvious from Figure 2 that the probability of damage is greater at lower temperatures. However, there is quite a fair bit of overlap in the distribution. Is launch temperature a real X (i.e., a real predictor of damage)? And if so, what is the probability of damage for any given launch temperature?

It is obvious that the probability of damage is greater at lower temperatures. However, there is quite a fair bit of overlap in the distribution. Is launch temperature a real X (i.e., a real predictor of damage)? And if so, what is the probability of damage for any given launch temperature?

Step 2. Formulate the Regression Model

Any regression requires a continuous output or Y. However, in this case the Y is discrete with only two categories or two events: Damage – yes or no. What to do? The “trick” behind the logistic regression is to turn the discrete output into a continuous output by calculating the probability (p) for the occurrence of a specific event. That means, the logistic regression provides a model to predict the p for a specific event for Y (here, the damage of booster rocket field joints, p = P[Y=1]) given any value of X (here, the temperature at the time of the launch). The logistic regression equation has the form:

This function is the so-called “logit” function where this regression has its name from. The procedure for modeling a logistic model is determining the actual percentages for an event as a function of the X and finding the best constant and coefficients fitting the different percentages.

This is exactly the equation that comes out of statistical software’s output for logistics regression:

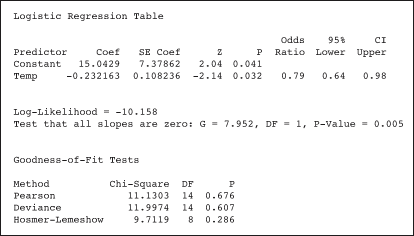
Step 3. Check Validity of Regression Model

There are two major checks that need to be done before it can said with confidence that this model is valid (please refer to the session output):

1. P-value for the coefficient is less than 0.05.
   A p-value is calculated for each coefficient. If the p-value is low then there is a significant relationship between the X variable and the Y. In this case, the coefficient for temperature has p-value of 0.032 (i.e., there is a significant relationship between the temperature and the probability of a damage).
2. P-value of the “goodness of fit” tests are greater than 0.05.
   Goodness-of-fit tests are conducted to see whether the model adequately fits the actual situation. Low p-values indicate a significant difference of the model from the observed data. Hence, the p-values should be above 0.05 to show that there are no significant differences between the predicted probabilities (from the model) and the observed probabilities (from the raw data). In this case, from the goodness-of-fit tests, none of them show a significant difference – the regression model is valid.

Step 4. Reverse the Logit Equation

This is done to obtain an answer to the question, given a particular setting of X, what is the probability of failure? Reversing this, the result is:

On the day of the Challenger incident, the temperature was 31 degree Fahrenheit. Hence, the probability of damage to the booster rocket field joints on that day is:

Damage was almost a certainty.

Step 5. Visualize the Results (Optional)

The event probability for all the possible temperature settings can be obtained by using statistical software. In Minitab software, for example, one must go to “Storage” and check the “Event Probability” box. The output is illustrated in Table 2.

Table 2: Event Probability
	Flight	Temp.	Damage	EPRO1
1	STS 1	66	0	0.430493
2	STS 2	70	1	0.229968
3	STS 3	69	0	0.273621
4	STS 5	68	0	0.322094
5	STS 6	67	0	0.374724
6	STS 7	72	0	0.158049
7	STS 8	73	0	0.129546
8	STS 9	70	0	*
9	STS 41B	57	1	0.859317

* are repetitions

Using this data, the scatter plot (decreasing logistic plot) in Figure 2 can be produced.