Key Points
- The Taguchi Method emphasizes robust design while considering customer satisfaction.
- It leverages experience and historical data to create better, cheaper products.
- Utilizing robust design methods allow you to cut through the noise to focus on what matters in a given product.
The Robust Design method, also called the Taguchi Method, pioneered by Dr. Genichi Taguchi, greatly improves engineering productivity.
By consciously considering the noise factors (environmental variation during the product’s usage, manufacturing variation, and component deterioration) and the cost of failure in the field the Robust Design method helps ensure customer satisfaction.
Robust Design focuses on improving the fundamental function of the product or process, thus facilitating flexible designs and concurrent engineering. Indeed, it is the most powerful method available to reduce product cost, improve quality, and simultaneously reduce development interval.
Why Use Robust Design Method?
Over the last five years, many leading companies have invested heavily in the Six Sigma approach to reduce waste during manufacturing and operations. These efforts have had a great impact on the cost structure and hence on the bottom line of those companies.
Many of them have reached the maximum potential of the traditional Six Sigma approach. What would be the engine for the next wave of productivity improvement?
Brenda Reichelderfer of ITT Industries reported on their benchmarking survey of many leading companies, “Design directly influences more than 70% of the product life cycle cost; companies with high product development effectiveness have earnings three times the average earnings; and companies with high product development effectiveness have revenue growth two times the average revenue growth.” She also observed, “40% of product development costs are wasted!”
These and similar observations by other leading companies are compelling them to adopt improved product development processes under the banner Design for Six Sigma.
The Design for Six Sigma approach focuses on 1) increasing engineering productivity so that new products can be developed rapidly and at low cost, and 2) value-based management.
Robust Design method is central to improving engineering productivity. Pioneered by Dr. Genichi Taguchi after the end of the Second World War, the method has evolved over the last five decades.
Many companies around the world have saved hundreds of millions of dollars by using the method in diverse industries: automobiles, xerography, telecommunications, electronics, software, etc.
Typical Problems Addressed By Robust Design
A team of engineers was working on the design of a radio receiver for ground-to-aircraft communication requiring high reliability, i.e., low bit error rate, for data transmission. On the one hand, building a series of prototypes to sequentially eliminate problems would be forbiddingly expensive.
On the other hand, computer simulation effort for evaluating a single design was also time-consuming and expensive. Then, how can one speed up development and yet assure reliability?
In another project, a manufacturer introduced a high-speed copy machine to the field only to find that the paper feeder jams almost ten times more frequently than what was planned.
The traditional method for evaluating the reliability of a single new design idea took several weeks. How can the company conduct the needed research in a short time and come up with a design that would not embarrass the company again in the field?
The Robust Design method has helped reduce the development time and cost by a factor of two or better in many such problems.
In general, engineering decisions involved in product/system development can be classified into two categories:
- Error-free implementation of the past collective knowledge and experience
- Generation of new design information, often for improving product quality/reliability, performance, and cost.
While CAD/CAE tools are effective for implementing past knowledge, the Robust Design method greatly improves productivity in the generation of new knowledge by acting as an amplifier of engineering skills. With Robust Design, a company can rapidly achieve the full technological potential of its design ideas and achieve higher profits.
Robustness Strategy
Variation reduction is key to reliability and productivity improvement. There are many approaches to reducing the variability, each one having its place in the product development cycle.
By addressing variation reduction at a particular stage in a product’s life cycle, one can prevent failures in the downstream stages.
The Six Sigma approach has made tremendous gains in cost reduction by finding problems that occur in manufacturing or white-collar operations and fixing the immediate causes. The robustness strategy is to prevent problems through optimizing product designs and manufacturing process designs.
Real-World Applications
The manufacturer of a differential op-amplifier used in coin telephones faced the problem of excessive offset voltage due to manufacturing variability.
High offset voltage caused poor voice quality, especially for phones further away from the central office. So, how to minimize field problems and associated costs? There are many approaches:
- Compensate the customers for their losses.
- Screen out circuits with large offset voltage at the end of the production line.
- Institute tighter tolerances through process control on the manufacturing line.
- Change the nominal values of critical circuit parameters such that the circuit’s function becomes insensitive to the cause, namely, manufacturing variation.
The approach 4 is the robustness strategy. As one moves from approach 1 to 4, one progressively moves upstream in the product delivery cycle and also becomes more efficient in cost control. Hence it is preferable to address the problem as upstream as possible.
The robustness strategy provides the crucial methodology for systematically arriving at solutions that make designs less sensitive to various causes of variation. It sees use in optimizing product design as well as in manufacturing process design.
Five Tools of Robust Design
The Robustness Strategy uses five primary tools:
- The P-Diagram classifies product variables into noise, control, signal (input), and response (output) factors.
- Ideal Function specifies the ideal form of the signal-response relationship as embodied by the design concept for making the higher-level system work perfectly.
- Quadratic Loss Function (also known as Quality Loss Function) quantifies the loss incurred by the user due to deviation from target performance.
- Signal-to-Noise Ratio predicts the field quality through laboratory experiments.
- Orthogonal Arrays gather dependable information about control factors (design parameters) with a small number of experiments.
P-Diagram
P-Diagram is a must for every development project. It is a way of succinctly defining the development scope. First, we identify the signal (input) and response (output) associated with the design concept.
For example, in designing the cooling system for a room the thermostat setting is the signal and the resulting room temperature is the response.
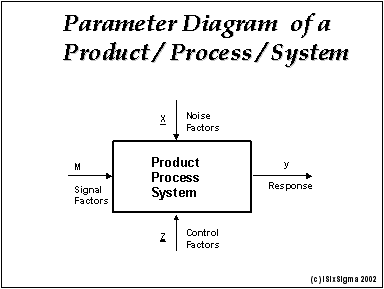
Next, consider the parameters/factors that are beyond the control of the designer. These are noise factors. Outside temperature, opening/closing of windows, and number of occupants are examples of noise factors.
Further, the designer also specifies parameters as control factors. The number of registers, their locations, the size of the air conditioning unit, and insulation are examples of control factors.
Ideally, the resulting room temperature should be equal to the set point temperature. Thus the ideal function here is a straight line of slope one in the signal-response graph. This relationship must hold for all operating conditions. However, the noise factors cause the relationship to deviate from the ideal.
Testing
The job of the designer is to select appropriate control factors and their settings so that the deviation from the ideal is minimal at a low cost. Such a design is called a minimum sensitivity design or a robust design. It can be achieved by exploiting the nonlinearity of the products/systems.
The Robust Design method prescribes a systematic procedure for minimizing design sensitivity and it is called Parameter Design.
An overwhelming majority of product failures and the resulting field costs and design iterations come from ignoring noise factors during the early design stages. The noise factors crop up one by one as surprises in the subsequent product delivery stages causing costly failures and band-aids.
These problems are avoided in the Robust Design method by subjecting the design ideas to noise factors through parameter design.
The next step is to specify the allowed deviation of the parameters from the nominal values. It involves balancing the added cost of tighter tolerances against the benefits to the customer.
Similar decisions must be made regarding the selection of different grades of the subsystems and components from available alternatives. The quadratic loss function is very useful for quantifying the impact of these decisions on customers or higher-level systems. The process of balancing the cost is called Tolerance Design.
The result of using parameter design followed by tolerance design is successful products at low cost.
Quality Measurement
In quality improvement and design optimization, the metric plays a crucial role. Unfortunately, a single metric does not serve all stages of product delivery.
It is common to use the fraction of products outside the specified limits as the measure of quality. Though it is a good measure of the loss due to scrap, it miserably fails as a predictor of customer satisfaction. The quality loss function serves that purpose very well.
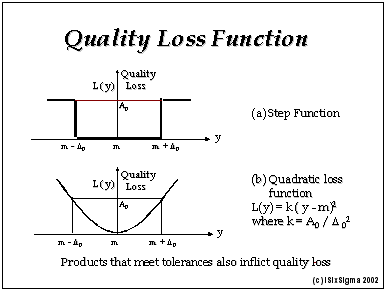
Let us define the following variables:
m: target value for a critical product characteristic
+/- Delta0: allowed deviation from the target
A0: loss due to a defective product
Then the quality loss, L, suffered by an average customer due to a product with y as the value of the characteristic is given by the following equation:
L = k * ( y – m )2
where k = ( A0 / Delta02 )
If the output of the factory has distribution of the critical characteristic with mean m and variance s2, then the average quality loss per unit of the product is given by:
Q = k { ( mu – m )2 + sigma2 }
Signal To Noise (S/N) Ratios
The product/process/system design phase involves deciding the best values/levels for the control factors. The signal-to-noise (S/N) ratio is an ideal metric for that purpose.
The equation for average quality loss, Q, says that the customer’s average quality loss depends on the deviation of the mean from the target and also on the variance. An important class of design optimization problems requires minimization of the variance while keeping the mean on target.
Between the mean and standard deviation, it is typically easy to adjust the mean on target, but reducing the variance is difficult. Therefore, the designer should minimize the variance first and then adjust the mean on target.
Among the available control factors, most of them should be used to reduce variance. Only one or two control factors are adequate for adjusting the mean on target.
The design optimization problem can be solved in two steps:
1. Maximize the S/N ratio, h, defined as
h = 10 log10 ( h2~ / sigma2 )
This is the step of variance reduction.
2. Adjust the mean on target using a control factor that does not affect h. Such a factor is called a scaling factor. This is the step of adjusting the mean on target.
One typically looks for one scaling factor to adjust the mean on target during design and another for adjusting the mean to compensate for process variation during manufacturing.
Static vs. Dynamic S/N Ratios
In some engineering problems, the signal factor is absent or it takes a fixed value. These problems are called Static problems and the corresponding S/N ratios are called static S/N ratios. The S/N ratio is described in the preceding section as a static S/N ratio.
In other problems, the signal and response must follow a function called the ideal function. In the cooling system example described earlier, the response (room temperature) and signal (set point) must follow a linear relationship.
Such problems are called dynamic problems and the corresponding S/N ratios are called dynamic S/N ratios.
The dynamic S/N ratio will be illustrated in a later section using a turbine design example.
Dynamic S/N ratios are very useful for technology development, which is the process of generating flexible solutions that can be used in many products.
Why It Matters
So, why should you focus on robust design? As previously discussed, it gets past a lot of the iterative approaches to product design. By accounting for every possible variable you can focus in on what matters the most in the deliverables you’re sending off to customers.
Steps in Robust Parameter Design
Robust Parameter design has 4 main steps:
1. Problem Formulation
This step consists of identifying the main function, developing the P-diagram, defining the ideal function and S/N ratio, and planning the experiments. The experiments involve changing the control, noise, and signal factors systematically using orthogonal arrays.
2. Data Collection/Simulation
The experiments may be conducted in hardware or through simulation. It is not necessary to have a full-scale model of the product for experimentation. It is sufficient and desirable to have an essential model of the product that adequately captures the design concept. Thus, the experiments can be done more economically.
3. Factor Effects Analysis
The effects of the control factors are calculated in this step and the results are analyzed to select the optimum setting of the control factors.
4. Prediction/Confirmation
To validate the optimum conditions we predict the performance of the product design under baseline and optimum settings of the control factors. Then we perform confirmation experiments under these conditions and compare the results with the predictions. If the results of confirmation experiments agree with the predictions, then we implement the results. Otherwise, the above steps must be iterated.
See Also: Robust Design Case Studies
Other Useful Tools and Concepts
While we’ve discussed the Taguchi Method at length, that’s only scratching the surface of what robust design has to offer. If you’d like to see how the Taguchi Method can simplify your experimental design process, I heavily recommend reading over our article on the subject.
Further, you might want to look into how the value index works. This allows you to readily concentrate your efforts on key areas of a project while cutting through the chaff.
Conclusion
The Robust Design Method works wonders for reducing variation in your production line. There are a fair few moving parts to consider, however. That said, mastering these steps is a sure-fire way to guarantee quality in your deliverables while making your customers happy.
