Much of the Six Sigma DMAIC methodology is concerned with finding differences: Do people do a certain job the same way or are there differences? Will a particular change make a difference in the output? Are there differences in where and when a problem occurs?

In most cases, the answer to all these questions is yes. People will do things differently. Process changes will affect output. A problem will appear in some places and not others.

That is why the more important question is often “does the difference really matter?” (Or, as statisticians would say, “Are the differences significant?”) When trying to compare results across different processes, sites, operators, etc., an hypothesis testing tool that can be used to help answer that question is the analysis of variance (ANOVA).

While the theory behind ANOVA can get complicated, the good news for Six Sigma practitioners with little experience is that most of the analysis is done automatically by statistical software, so no one has to crunch a lot of numbers. Better still, the software usually produces a simple chart that visually depicts the degree of difference between items being compared – making it easy to interpret and explain to others.

A simple case study shows ANOVA in action.

The Question: Which Site Is Fastest?

Table 1: Collected Data
Site A	Site B	Site C
Time in minutes to complete five loan applications
15	28	26
17	25	23
18	24	20
19	27	17
24	25	21

In order to optimize the loan application process across three branches, a company wants to know which of the three locations handles the process the most efficiently. Once it determines which site is consistently fastest, the company plans to study what that site does, and adapt what it learns to the other sites. In the adjacent table is a sample of the data collected. (In real life, it is likely that more than five data points per location would be collected, but this is a simple example to illustrate the principles.)

A quick glance at this data would probably lead to the conclusion that Site B is considerably slower than Site A. (The differences are usually much harder to detect when there are a lot more data points.) But is it different from Site C? And are A and C really different?

The ANOVA Analysis

To understand the calculations performed in an ANOVA test, a person would need to study up on statistical topics like “degrees of freedom” and “sum of squares.” Fortunately, to interpret the results, a person only needs to understand three basic concepts:

1. Mean: The mathematical average of a set of values.
2. Standard deviation: A value that represents a typical amount of variation in a set of data. (“Sigma” is the statistical notation used to represent one standard deviation; the term “Six Sigma” is used to indicated that a process is so good that six standard deviations – three above and three below the mean – fit within the specification limits)
3. p-value: A term used in hypothesis testing to indicate how likely it is that the items being compared are the same. A low p-value – often anything below 0.05 – indicates that it is very unlikely the items are the same. (Or, as non-statisticians would say, “They are different.”)

The output from the statistical software is in two parts. Figure 1 shows the first portion:

As can be seen, the p-value here is .007, a very small value. That shows that all three sites are not the same, but it does not indicate in what ways they differ. For that, the second part of the ANOVA output needs to be examined (Figure 2).

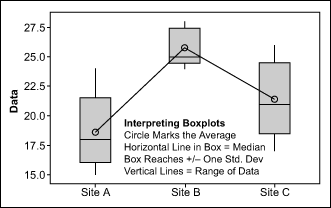
The graphical output from the ANOVA analysis is easy to interpret once the format being used by the statistical program is understood. The example in Figure 2 is a boxplot, typical output from statistical software.

The two key features of a boxplot are the location of the circles, denoting the mean or average for each site, and the range of the shaded gray boxes, which are drawn at plus and minus one standard deviation. Compare where the circle (average) for item falls relative to the gray boxes for the other items. If the two overlap, then they are not “statistically different.” If they do not overlap, it can be concluded that they are different.

In this case, for example, the circle (average) for Site C falls within the values marked by the gray box for Site A. So based on this data, Site A is not statistically different from Site C. However, the circle (average) for Site B does not fall within the gray-box values for either Site A or Site C, so it is significantly different from those sites.

Acting on the Results of ANOVA

Knowing that the goal was to optimize the loan application times, what path should be taken, given these results? Odds are that there are major differences in how Site B handles the loan applications compared to Site A and Site C. At the very least, the company would want to bring Site B up to the speed of the other two sites. Thus, the first step would be to compare the loan application processes across all three sites and see how Site B differs in its policies or procedures. Once all three sites were operating the same way, then the company can look for further improvements across the board.

Conclusion: Aid for Improve Phase

In Six Sigma projects, one of the biggest challenges is often whether the differences which are observed are significant enough to warrant action. One often overlooked tool that helps project teams make definitive conclusions is ANOVA. Analysis of variance is appropriate whenever continuous data from two or more groups or categories are being compared.

A better understanding of the calculations used to generate the numerical and graphical results can be found in the book Statistics for Experiments by George Box, et al. Or, those using ANOVA for the first time should be able to get help setting up the data in a statistical software program from an experienced Black Belt or Master Black Belt.

However, as shown in the example, both the numerical and graphical output from the ANOVA tests are easy to interpret. The knowledge gained will help the project team plan its improvement approach.