An arbitrary and statistically flawed tie-breaking rule cost Nastia Liukin of the United States the gold medal in the women’s uneven bars competition at the Olympics earlier this month, according to Dr. Prasad Raje, CEO of Instantis.

After looking at the tied scores of gymnasts Liukin and He Kexin of China, Raje figures that Liukin actually had a “statistically superior score because there was less variance in the judge’s opinions on who performed better.”

The gymnasts scored the same down to the third decimal place by using the average score from six judges and throwing out the high and low score. So Liukin had scores of 9, 9, 9 and 9.1, and Kexin had scores of 9.1, 9.1, 8.9 and 9. According to the tie-break rule, the winner is determined by throwing out the low score of the four valid remaining scores. As a result, a 9.0 was dropped from Liukin’s scores and an 8.9 from Kexin’s. This meant the outcome was based on the opinions of only three judges – and tilted the gold in favor of Kexin.

Instead of throwing out data points, the judges should have kept all the valid data points, and done a statistical analysis of the “quality” of the data, Raje says. Here’s a figure he developed:

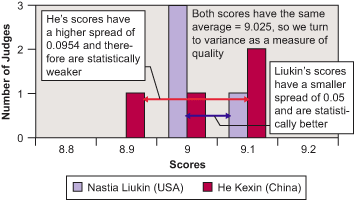
The statistical spread in Liukin’s scores is significantly lower (0.0500) than that of Kexin’s (0.0954). Therefore, according to Raje, Liukin should have got the gold medal.

This shows that those who run the Olympics might find it to their advantage to add a Six Sigma practitioner to their rules committee.