Attribute control charts arise when items are compared with some standard and then are classified as to whether they meet the standard or not. The control chart is used to determine if the rate of nonconforming product is stable and detect when a deviation from stability has occurred. The argument can be made that a LCL should not exist, since rates of nonconforming product outside the LCL is in fact a good thing; we WANT low rates of nonconforming product. However, if we treat these LCL violations as simply another search for an assignable cause, we may learn for the drop in nonconformities rate and be able to permanently improve the process.
p Charts can be used when the subgroups are not of equal size. The np chart is used in the more limited case of equal subgroups.
Steps in Constructing a p Chart
- Determine the size of the subgroups needed. The size, n(i), has to be sufficiently large to have defects present in the subgroup most of the time. If we have some idea as to what the historical rate of nonconformance, p, is we can use the following formula to estimate the subgroup size:
n=3/p
- Determine the rate of nonconformities in each subgroup by using:
- Find pbar; there are k subgroups.
- Estimate sigma-p if needed and determine the UCL and LCL:
- Plot the centerline, pbar, the LCL and UCL, and the process measurements, the phat’s.
- Interpret the data to determine if the process is in control.
phat(i)=x(i)/n(i)
where:
phat(i)=the rate of nonconformities in subgroup i
x(i)=the number of nonconformities in subgroup i
n(i)= the size of subgroup i
![]()
![]()
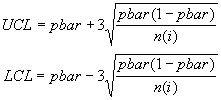
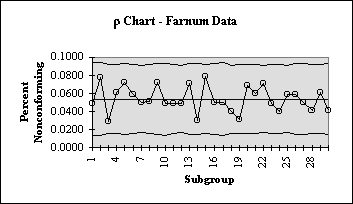
Example:
Farnum Example:
data is from Farnum (1994):
Modern Statistical Quality Control and Improvement, p. 242
Number
Day Rejects Tested Proportion
1 14 286 0.0490
2 22 281 0.0783
3 9 310 0.0290
4 19 313 0.0607
5 21 293 0.0717
6 18 305 0.0590
7 16 322 0.0497
8 16 316 0.0506
9 21 293 0.0717
10 14 287 0.0488
11 15 307 0.0489
12 16 328 0.0488
13 21 296 0.0709
14 9 296 0.0304
15 25 317 0.0789
16 15 297 0.0505
17 14 283 0.0495
18 13 321 0.0405
19 10 317 0.0315
20 21 307 0.0684
21 19 317 0.0599
22 23 323 0.0712
23 15 304 0.0493
24 12 304 0.0395
25 19 324 0.0586
26 17 289 0.0588
27 15 299 0.0502
28 13 318 0.0409
29 19 313 0.0607
30 12 289 0.0415Calculations:
PBAR = 0.0539
UCL = pbar + 3*sqrt(pbar*(1-pbar)/n(i))
LCL = pbar - 3*sqrt(pbar*(1-pbar)/n(i))
Day CL UCL LCL Proportion
1 0.0539 0.093892049 0.013808661 0.0490
2 0.0539 0.094246721 0.013453989 0.0783
3 0.0539 0.092310827 0.015389883 0.0290
4 0.0539 0.092126068 0.015574642 0.0607
5 0.0539 0.093410843 0.014289867 0.0717
6 0.0539 0.092624795 0.015075915 0.0590
7 0.0539 0.091587368 0.016113342 0.0497
8 0.0539 0.091943946 0.015756764 0.0506
9 0.0539 0.093410843 0.014289867 0.0717
10 0.0539 0.093822229 0.013878481 0.0488
11 0.0539 0.092498288 0.015202422 0.0489
12 0.0539 0.091240619 0.016460091 0.0488
13 0.0539 0.093209857 0.014490853 0.0709
14 0.0539 0.093209857 0.014490853 0.0304
15 0.0539 0.091883814 0.015816896 0.0789
16 0.0539 0.09314354 0.01455717 0.0505
17 0.0539 0.094103724 0.013596986 0.0495
18 0.0539 0.091646103 0.016054607 0.0405
19 0.0539 0.091883814 0.015816896 0.0315
20 0.0539 0.092498288 0.015202422 0.0684
21 0.0539 0.091883814 0.015816896 0.0599
22 0.0539 0.091528906 0.016171804 0.0712
23 0.0539 0.092688517 0.015012193 0.0493
24 0.0539 0.092688517 0.015012193 0.0395
25 0.0539 0.091470715 0.016229995 0.0586
26 0.0539 0.093683678 0.014017032 0.0588
27 0.0539 0.093011904 0.014688806 0.0502
28 0.0539 0.091823966 0.015876744 0.0409
29 0.0539 0.092126068 0.015574642 0.0607
30 0.0539 0.093683678 0.014017032 0.0415p - Chart: