
Preparing Individuals Charts
An Individuals Chart is used when the nature of the process is such that it is difficult or impossible to group measurements into subgroups so an estimate of the process variation can be determined. This occurs frequently in low volume production situations and in situations in which continuously varying quantities within the process are process-related variables.
The solution is to artificially create subgroups from the data and then calculate the range of each subgroup. This is done by creating rolling groups (most often pairs) of data through time and using the pairs to determine the range R. The resulting ranges are called moving ranges.
Steps in Constructing an Individuals Chart
- A moving range average is calculated by taking pairs of data (x1,x2), (x2,x3), (x3,x4),…, (xn-1,xn), taking the sum of the absolute value of the differences between them and dividing by the number of pairs (one less than the number of pieces of data). This is shown mathematically as:
- An estimate of the process standard deviation is given by
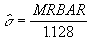
and the three sigma control limits become:
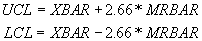
- Plot the centerline, XBAR, LCL, UCL, and the process measurement X(i).
- Interpret the data using the following guidelines to determine if the process is in control:
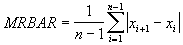
a. one point outside the 3 sigma control limits
b. eight successive points on the same side of the centerline
c. six successive points that increase or decrease
d. two out of three points that are on the same side of the centerline, both at a distance exceeding 2 sigmas from the centerline
e. four out of five points that are on the same side of the centerline, four at a distance exceeding 1 sigma from the centerline
f. using an average run length (ARL) for determining process anomalies
Some Additional Notes:
If the process has been brought into statistical control, the sample standard deviation, s/c(4), can well be used as an estimate of the process standard deviation sigma. This works well unless there are trends in the data (which cause an inflated value of s). When one is certain that no trends exist in the data, s/c(4), will provide considerable more power than MRBAR/1.128. This means that one is more likely to detect out-of-control situations when they exist.
Example:
The following data consists of 20 sets of three measurements of the diameter of an engine shaft. An R-Chart will be used to examine variability followed by a Median Chart.
n meas#1 MR 1 2.0000 0.0002 2 1.9998 0.0000 3 1.9998 0.0001 4 1.9997 0.0006 5 2.0003 0.0001 6 2.0004 0.0006 7 1.9998 0.0002 8 2.0000 0.0005 9 2.0005 0.0010 10 1.9995 0.0007 11 2.0002 0.0000 12 2.0002 0.0002 13 2.0000 0.0000 14 2.0000 0.0006 15 1.9994 0.0005 16 1.9999 0.0003 17 2.0002 0.0002 18 2.0000 0.0003 19 1.9997 0.0006 20 2.0003 INDIVIDUALS CHART LIMITS: XBAR = 2.0000 MRBAR = 0.0004 UCL = XBAR + 2.66*MRBAR = 2.000+2.66*.0004 = 2.001064 LCL = XBAR - 2.66*MRBAR = 2.000-2.66*.0004 = 1.997872
Individuals Chart:
