
A binomial distribution can be described as the probability of a binary outcome in an activity that is repeated multiple times. It is a distribution of discrete data rather than continuous data. For example, a coin toss has only two possible discrete outcomes: heads or tails. Inspecting and testing a manufactured part can have two outcomes: pass or fail.
Your salesperson either sold the customer or didn’t sell the customer. Saying they “almost got the sale” or “just missed getting the sale” is a meaningless statement. They either sold the job or failed to sell the job.
Overview: What is a binomial distribution?
The formula for the binomial distribution is:
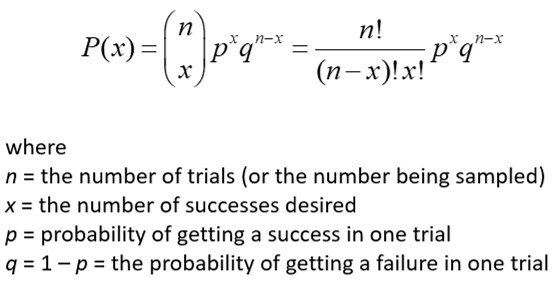
Binomial distributions must meet the following four criteria:
- Each outcome can only be one of two categories called a success or failure.
- There is a fixed number of observations.
- Each observation is independent of each other.
- The probability of success (p) for each observation is the same.
Under certain circumstances, you can use the normal distribution to approximate the binomial distribution. According to the Central Limit Theorem, the sampling distribution of the sample means becomes approximately normal if the sample size is large enough.
The first step for using the normal approximation to the binomial is to be sure your sample size is large enough. You can determine this with two calculations: n * p and n * q. When n * p and n * q is greater than 5, you can use the normal approximation to the binomial to solve a problem.
An industry example of a binomial distribution
The quality control manager was trying to determine the probability of shipping defective products to the customer after the parts are inspected. His historical data shows that inspection has been 95% effective in preventing bad products from being shipped. He wanted to know the probability of finding 95 or less good parts in a random sample of 100 parts. Below is an online calculator you can use to solve this type of problem.
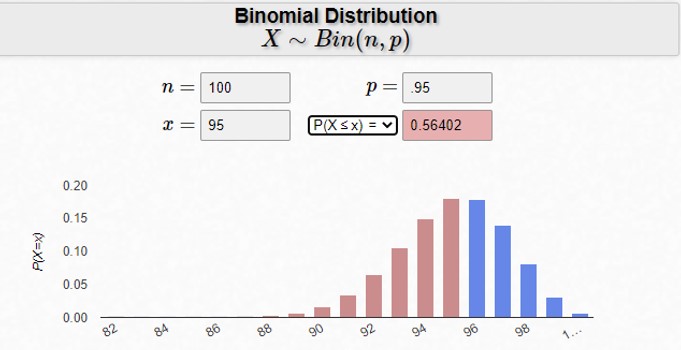
The manager was concerned since his inspection system was intended to find and sort out defective parts. The results of the calculator showed that, out of 100 parts inspected, there was a 56% probability that more than 5% will be defective. This was in excess of the assumed 95% effectiveness of his inspection system.
Frequently Asked Questions (FAQ) about a binomial distribution
Can I use the binomial distribution if I have 3 unique possible outcomes?
No. The bi in binomial means you can only have two outcomes.
What does the output of the binomial formula give me?
It gives you the probability (p) of what you have defined as a success. If you want to know the probability of what you have defined as a failure (q) you can use the value of 1-p.
What if my next outcome depends on the previous outcome, can I use the binomial to predict probabilities?
No. One of the primary criteria for using the binomial is that each trial or occurrence is independent of all other trials.