
If there is a standard order, does that mean there’s a non-standard order? No, but this article will explain what standard order is, when to use it, and when not to. You will learn some of the benefits of using standard order in your design of experiments (DOE) and a few hints on how to decide whether to use it or not.
Overview: What is standard order?
Standard order is defined as the non-random sequence of your experimental runs for a multi-factor, multi-level full factorial or fractional factorial DOE.
Let’s say you were interested in whether machine speed, temperature, and pressure had an effect on the bonding of your laminated glass panels. Based on your previous work in the analyze phase of DMAIC, you decided to run your experiment at a speed of 100 fpm and 150 fpm, temperature at 150F and 200F, and your pressure at 80 psi and 90 psi. The question is, how many total unique combinations of those settings are there?
The formula to calculate the number of combinations is Levels^Factors, or in our example, 2^3 = 8. By coding each level as either a minus (low or current setting) or plus (high or new setting), we can create a sequenced list of the runs.
This is how it would look, and it’s called the standard order of the runs.

Note the pattern of plus and minus notation. For the first factor it is -, + in sequence. For the second factor it is -, – then +, +. For the third factor it is four minus then four plus. If you added a fourth factor, you would have 16 runs (2^4), and the same sequence repeats for the first three factors, with the new factor being 8 minus followed by 8 plus.
You can also see that the + and – settings are run an equal number of times: four minus and four plus. This orthogonality, or balance, of the design is important for running a valid experiment. Using our example, your first run would consist of setting speed at 100 fpm (-), temperature at 150F (-), and pressure at 80 psi (-).
But, you rarely use the standard order. Instead, you would randomize the sequence of the eight runs. If you conducted these eight runs over the course of the day, you see that all the minus runs for pressure were in the morning, and the plus runs in the afternoon.
If there happened to be a lurking variable, such as building temperature, you would be doing your first four runs when it was cool in the morning, and the last four when it was warmer in the afternoon. Since you didn’t include building temperature in your experiment, you don’t know if it has an effect.
By randomizing the runs over the course of the day, you block out the effect of building temperature. This allows you to focus your experiment on your identified factors of machine speed, temperature, and pressure.
2 benefits and 1 drawback of standard order
While doing your experiment in standard order has some benefits, there is a significant downside.
1. Easy to determine
By utilizing the standard order pattern of plus and minus, you are able to identify the possible combination of factor runs regardless of the number of factors.
2. Consistent
The determination of the standard order of runs is the same no matter who does it or where. The same pattern of plus and minus will always represent the sequence of runs.
3. Does not account for the possibility of a lurking variable
If there is a factor or variable you are not including in your DOE, the later factors in the list may introduce experimental noise because of the sequence of the standard order. The purpose of randomizing the standard order runs is to eliminate or block any lurking variables.
Why is standard order important to understand?
Standard order represents the non random sequence of runs for a design of experiments. Understanding what it means is an important consideration for the final design of your experiment.
Pattern
The repeating pattern of the standard order allows you to determine the sequence of runs no matter how many factors you have.
Different when running a fractional factorial
The total number of runs from the standard order are not run in a fractional factorial design. Deciding which runs you will use requires an understanding of a balanced design.
Complexity
Once you start adding factor levels, the amount of runs dramatically increases. The eventual selection of the sequence will be more complicated than a simple two-level experiment.
An industry example of standard order
The Master Black Belt (MBB) employed by a medium-size trucking company was tasked with determining whether the average driving speed, octane of the fuel, and tire pressure had an effect on the miles per gallon of truck performance.
A two-level design was selected for this three-factor experiment. Shown below is the standard order table.
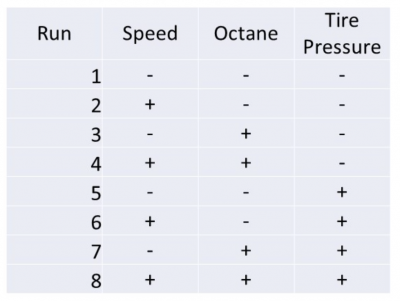
The MBB immediately noticed there could be a problem if he ran the experiment in this standard order. Since the company was based in Phoenix, he knew the road temperature would vary during the course of the day. This would have impacted the tire pressure readings since he had the – or low readings all being done in the morning and the + or high readings done in the heat of the afternoon. Since he didn’t want to include road temperature as a variable, he randomized the runs.
All the information was entered into a popular software package that produced the worksheet ready for carrying out the experimental runs (below). You can compare the standard order sequence with the actual randomized runs. The circled lines show that the first standard order run was actually the fifth experiment, and the last standard order run was done fourth.

3 best practices when thinking about standard order
Follow these tips on how to develop and deal with the implications of the standard order of your experimental runs.
1. Try to keep your design to two levels if you can
Not only will your standard order get more complicated to develop, but your costs and time will dramatically increase with the addition of levels.
2. Start with the low condition first
Convention calls for you to start your standard order list with the minus (low or current) condition for all the factors. Then you can proceed to incorporate the standard pattern.
3. Randomize rather than use the standard order
The old saying is, “Block what you can, randomize what you cannot.” Use randomization when trying to mitigate the effect of unwanted factors or variables you are not interested in.
Frequently Asked Questions (FAQ) about standard order
1. What is standard order?
Standard order is a technique in design of experiments that lists the sequenced, non-random combinations of factors and levels.
2. Is there a specific pattern to standard order?
Yes. The following table illustrates the standard order of a three factor, two-level experiment where the minus represents the coded level of the low setting and the plus the high setting. You can see the alternating pattern of the plus and minus characters.

3. Should I run my design of experiments in the sequence of the standard order?
It’s not recommended because you could be allowing a lurking or unwanted noise variable to influence your experiment. It’s better to randomize the runs rather than use the sequence of the standard order.
Final thoughts on standard order
The non random sequence of runs in a design of experiments is called the standard order of the experiment. It is typically represented by a series of plus and minus signs. This series follows a consistent pattern and is easily developed and expanded with the addition of other factors.
Since it may introduce some bias due to the noise of unwanted variables, it is recommended that you randomize the sequence of the standard order when you run your experiment.