
Nonparametric or distribution-free methods have several advantages or benefits. They may be used on all types of data including nominal, ordinal, interval and ratio scaled. They make fewer and less stringent assumptions than their parametric counterparts. Depending on the particular procedure, nonparametric methods may be almost as powerful as the corresponding parametric procedure when the assumptions of the latter are met. When this is not the case, they are generally more powerful.
A parametric method – Consider using when:
- The assumptions for the population probability distribution hold true
- The sample size is large enough for the central limit theorem to lead to normality of averages
- The data is non-normal but can be transformed
A nonparametric method – Consider using if the data is:
- Distinctly non-normal and cannot be transformed
- From a sample that is too small for the central limit theorem to lead to normality of averages
- From a distribution not covered by parametric methods
- From an unknown distribution
- Nominal or ordinal
A False Sense of Security
Black Belts may have a false sense of security when using nonparametric methods because it is generally believed that nonparametric tests are immune to data assumption violations and the presence of outliers. While nonparametric methods require no assumptions about the population probability distribution functions, they are based on some of the same assumptions as parametric methods, such as randomness and independence of the samples.
In addition, many nonparametric tests are sensitive to the shape of the populations from which the samples are drawn. For example, the 1-sample Wilcoxon test can be used when the team is unsure of the population’s distribution but the distribution is assumed to be symmetrical. For the Kruskal-Wallis test, samples must be from populations with similar shapes and equal variances. The Kruskal-Wallis test is more powerful than the Mood’s Median test for data from many distributions, but is less robust against outliers.
Table 1 contains the most commonly used parametric tests, their nonparametric equivalents and the assumptions that must be met before the nonparametric test can be used.
| Table 1: Parametric, Nonparametric Equivalents and Assumptions | ||
| Parametric Statistical Test | Nonparametic Equivalents | Nonparametric Data Assumptions |
| 1-Sample z-Test or 1-Sample t-Test |
1-Sample Sign Test 1-Sample Wilcoxon Test |
Bivariate random variables are mutually independent. The measurement scale is at least ordinal.
Random, independent sample is from a population with a symmetric distribution. |
| 2-Sample t-Test |
Mann-Whitney | Mutually independent random samples from two populations that have the same shape, whose variances are equal and a scale that is ordinal. |
| Paired t-Test |
Paired Wilcoxon Test |
Random, independent samples are from populations with symmetric distributions. |
| One-Way Analysis of Variance (ANOVA) | Kruskal-Wallis Test Mood’s Median Test |
Random, mutually independent samples are from populations whose distribution functions have the same shape, equal variances. Each sample consists of five or more measures. Kruskal-Wallis is more powerful than Mood’s for data from many distributions, but less robust against outliers.
Independent random samples from population distributions that have the same shape. Mood’s Median test is robust against outliers. |
| Two-Way ANOVA | Friedman Test | Responses for each of the block-treatments are from populations whose distribution functions have the same shape and equal variances. Treatments must be randomly assigned within the blocks. |
The figure below provides a roadmap for selecting the appropriate nonparametric method.
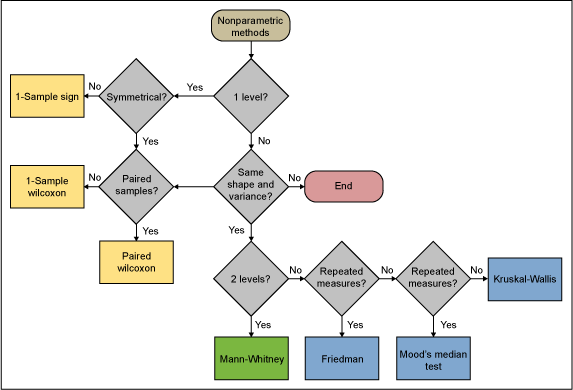
Conclusion: Can Be More Powerful…
Nonparametric methods are essential tools in the Black Belt’s analytic toolbox. When appropriately applied, nonparametric methods are often more powerful than parametric methods if the assumptions for the parametric model cannot be met.