To generate a valuable customer survey, practitioners should follow nine steps. Part One of this series discussed the first three steps: establishing a goal, determining the sample and choosing the methodology. Part Two covered the fourth, fifth and sixth steps, which related to what types of questions to ask and how they should be asked. The final three steps, which follow the survey through its execution and analysis of results, are explored here.
Step 7: Pre-testing the Survey
A pre-test is a small-scale implementation of the questionnaire. The test is critical for identifying problems that both respondents and survey administrators may encounter. The purpose of the pre-test is to gain feedback, not to be statistically accurate; thus, sample size is not a major consideration. However, who is selected to participate in the pre-test is important. Practitioners should aim for around 50 people – perhaps employees of the organization, who are similar to the target population – to test the survey.
The factors to evaluate in the pre-test are the clarity, comprehensiveness and acceptability of the survey.
- Clarity – Are the questions and responses understood? Are there any ambiguous questions?
- Comprehensiveness – Consider the target population when designing the questions. Make sure that the questions and responses cover the complete range of alternatives.
- Acceptability – Is the survey too long? Do any questions feel like an invasion of privacy? Does the survey appear to violate any moral or ethical conventions?
After the pre-test, revise the questions as needed. If there is considerable revision, you may want to conduct another pre-test. Once revisions have been completed, practitioners can begin to implement the survey.
Step 8: Administering the Survey
If they have followed the earlier steps, practitioners should already know the method of survey administration and have a project plan. They should ensure that all involved in the survey know what they have to do and include this training within the project plan. With regard to quality control, practitioners should not just sit back and wait for the results. They must remain engaged during the entire process. If something does go wrong, it is best to catch the problem as soon as possible.
The data collected from the survey should be presented in a succinct and meaningful way. This will assist in future analysis of the data. Two techniques to consider are the use of frequency distributions and contingency tables.
Frequency Distribution
A frequency distribution is a summary presentation of the frequency of a response for each category. The emphasis here is presenting only one variable. Frequency distributions typically contain the following:
- Number and title of the table
- Clearly labeled variable and categories
- Categories presented in a logical sequence (such as time or salary)
- The number of non-responses
- If there is an “Other” category, some form of description should be provided
An example is shown in the table below:
| Table 1: Frequency Distribution | ||
| Question: How long have you been employed with CSI DeLeeuw? | ||
| Time with CSI DeLeeuw |
f |
% |
| Less than 1 year | 30 | 23.6 |
| More than 1 year, less than 5 | 39 | 30.7 |
| More than 5 years, less than 10 | 34 | 26.8 |
| More than 10 years, less than 15 | 16 | 12.6 |
| 15 years or more | 8 | 6.3 |
| Total | 127 | 100.00 |
| Non-responses = 25 | ||
Contingency Tables
Unlike frequency distributions, contingency tables allow for simultaneous analysis of more than one variable. Contingency tables present the relationship between two variables and are referred to by their number of rows and columns. For example, a table with four rows and six columns would be a 4×6 contingency table.
The columns in a contingency table traditionally are for the independent variable. Practitioners should calculate percentages for the column variables and include both row and column totals. The following figures represent sample questions followed by the contingency table:
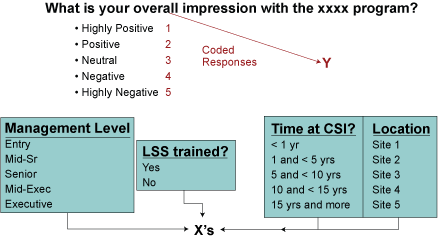
| Table 2: Contingency Table Based on Sample Survey Data | ||||||||||||
|
Entry |
Mid-Sr |
Senior |
Mid-Exec |
Executive |
Total |
|||||||
| Count | % | Count | % | Count | % | Count | % | Count | % | Count | % | |
| High Positive | 7 | 10.1 | 6 | 10.3 | 7 | 12.1 | 7 | 12.5 | 8 | 12.7 | 17 | 11.3 |
| Positive | 11 | 15.9 | 19 | 32.8 | 11 | 19.0 | 15 | 26.8 | 17 | 27.0 | 36 | 24.0 |
| Neutral | 21 | 30.4 | 18 | 31.0 | 22 | 37.9 | 16 | 28.6 | 20 | 31.7 | 48 | 32.0 |
| Negative | 24 | 34.8 | 8 | 13.8 | 12 | 20.7 | 12 | 21.4 | 13 | 20.6 | 34 | 22.7 |
| High Negative | 6 | 8.7 | 7 | 12.1 | 6 | 10.3 | 6 | 10.7 | 5 | 7.9 | 15 | 10.0 |
| Total | 69 | 100.0 | 58 | 100.00 | 58 | 100.0 | 56 | 100.0 | 63 | 100.0 | 150 | 100.0 |
Step 9: Analyzing the Results
There are multiple tests that can be used to assist with the analysis of the survey data, including the Chi-square test and proportion tests.
Chi-square
The 
(Chi-square) test is a measure of divergence of the observed and expected frequencies. Chi-square can be used as a:
- Goodness-of-fit test to determine if a sample of data is from a population with a specified distribution.
- Test of independence to determine the association between the rows and columns of a two-way table.
In this scenario, the test to determine whether the data observed differs from what could be expected due to chance. The c2 test will tell whether or not a relationship exists. There are three other tests that could give the strength of this relationship – Cramer’s V, Phi and Gamma tests for ordinal data – but these are more complicated.
There are two types of Chi-square test: 1-way and 2-way. The formula for both is:
, where
= the Chi-square statistic
O = the number of observed from each cell
E = the number of expected from each cell
= calculate the value for each cell, then add all these values
1-Way Test
For this test, just one column – observed data – is evaluated. Practitioners need to know what they should expect to see for each cell and the degrees of freedom. This test answers the question: Does the observed count differ from what could be expected due to chance?
For the test procedure, first state the hypotheses:
- Ho: There is no difference between observed and expected.
- Ha: There is a difference.
Next, specify the alpha (usually 0.05). Find the critical value for ( critical) for alpha and calculate (calculated). If: calculated > critical, reject Ho; otherwise, fail to reject and conclude no statistically significant differences.
2-Way Test
For this test, one column (independent variable) and one row (dependent variable) are evaluated. The data needs to be in contingency table form. This test can be completed using statistical analysis software and can answer the question: Is there a relationship between two categorical variables?
For this test procedure, the hypotheses are:
- Ho: No relation between column and row.
- Ha: There is a relation.
Next, specify the alpha (usually 0.05). Then, run the analysis in the software. If the p-value is less than 0.05, reject Ho; otherwise, fail to reject and conclude no statistically significant differences.
1-Proportion Test
A proportion is a ratio of occurrences, generally an occurrence of interest (X) compared to all occurrences (N). Confidence intervals provide practitioners with a proportional range in which it is possible to state (with a specified confidence) that the true population value will fall within. This test can answer the question: Is the observed proportion equal to some specified proportion?
The data in the chart below can be used to illustrate the use of a 1-proportion test.
| Table 3: Response Data | |
| High positive | 17 |
| Positive | 36 |
| Neutral | 48 |
| Negative | 34 |
| High negative | 15 |
| Total | 150 |
There were 53 total positive responses. Using statistical analysis software, it is possible to state with 95 percent certainty that the true population’s positive perception of the program falls between 27.7 percent and 43.5 percent.
Successful Completion
The knowledge gained from surveys can be invaluable in continuing a process improvement journey. Therefore, when conducting a survey, it is important that practitioners have a clear understanding of:
- What they want to learn from a survey and who they want to learn it from.
- What delivery method and question formats to use.
- How to present and analyze the survey findings.
With this information, practitioners will be prepared to write and execute a survey.
