
“All models are wrong but some are useful.” – George Box
The statistic R2 is useful for interpreting the results of certain statistical analyses; it represents the percentage of variation in a response variable that is explained by its relationship with one or more predictor variables.
Common Use of R2
When looking at a simple or multiple regression model, many Lean Six Sigma practitioners point to R2 as a way of determining how much variation in the output variable is explained by the input variable. For example, a simple regression model of Y = b0 + b1X with an R2 of 0.72 suggests that 72 percent of the variation in Y can be explained with the b0 + b1X equation. Multiple regression is the same except the model has more than one X (predictor) variable and there is a term for each X in the model; Y = b0 + b1X1 + b2X2 + b3X3.
Uncommon Use of R2
While Black Belts often make use of R2 in regression models, many ignore or are unaware of its function in analysis of variance (ANOVA) models or general linear models (GLMs). If the R2 value is ignored in ANOVA and GLMs, input variables can be overvalued, which may not lead to a significant improvement in the Y.
GLM Example
Suppose a process improvement team conducting a Lean Six Sigma project has created a process map and fishbone diagram; the team brainstormed potential Xs that impact a given Y. The team then systematically prioritized and narrowed the list down to four potential X variables to be analyzed further in the Analyze phase of DMAIC (Define, Measure, Analyze, Improve, Control). Subsequent hypothesis tests resulted in two critical Xs, both discrete (such as shift, product, day of week, etc.)
The data is analyzed using the GLM (see Figure 1).
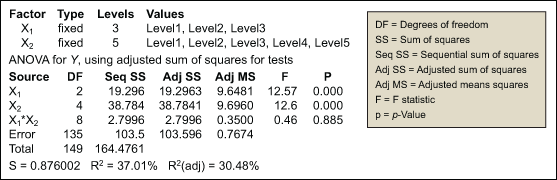
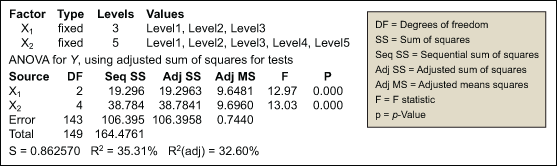
The analysis shows that the p-value for X1 * X2 is greater than 0.05, indicating no interaction between the two variables. Thus, the model will be reduced to eliminate the X1 * X2 term. Figure 2 displays the results of the reduced model.
The associated main effects plot and box plots are shown in Figure 3.
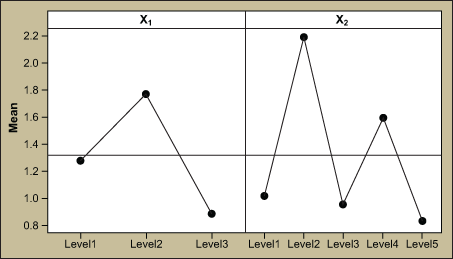
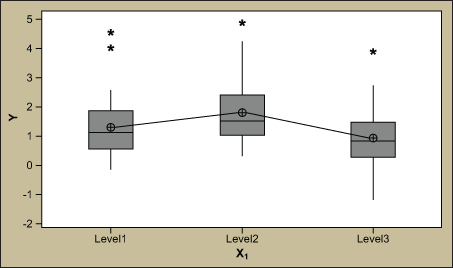
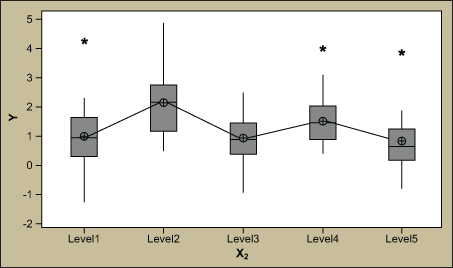
Since the p-values are less than 0.05 the team may very well celebrate the findings and make improvements to X1 and X2. Although the statistics and the output look promising, the R2 statistic tells a different story.
If the R2 statistic is ignored here, a team may veer off track and not find other critical Xs. Notice that the total adjusted R2 = 32.6 percent. Since only 32.6 percent of the variation is explained by X1 and X2, that means that 67.4 percent of the variation is unaccounted for! Part of this is measurement error, which should be minimal and evaluated with an appropriate gage R&R study. But the majority is noise – drivers that are not yet discovered and not in the analysis model.
In this scenario, the team discovered two critical Xs that were addressed in the Improve phase of the project only to discover that the changes did not make a meaningful improvement to the Y. Many practitioners have likely found themselves in this situation. Regrettably, such results can negatively impact both morale and credibility. Fortunately, making use of the R2 statistic can help prevent this problem.
R2: Ignore It, Regret It
While the p-values of factors analyzed with ANOVA or GLM can indicate significance, practitioners must also notice how much of the process variation those factors contribute. An assessment of unaccounted for terms must be investigated and their effect on process variation reduced before significant overall improvement can be realized. Ignoring the information provided by the R2 statistic may keep a business from achieving breakthrough results.