Consider a production process that produced 10,000 widgets in January and experienced a total of 100 rejected widgets after a quality control inspection (i.e., failure rate = 0.01, success rate = 0.99). A Six Sigma project was deployed to fix this problem and by March the improvement plan was in place. In April, the process produced 8,000 widgets and experienced a total of 72 rejects (failure = 0.009, success = 0.991). Did the process improve?
The Two-Proportions Test
The appropriate hypothesis test for this question is the two-proportions test. As the name suggests it is used when comparing the percentages of two groups. It only works, however, when the raw data behind the percentages (100 rejects out of 10,000 parts produced and 72 out of 8,000 respectively) is available since the sample size is a determining factor of the test statistics.
In our example, the null hypothesis (Ho) and the alternative hypothesis (Ha) are:
Ho: Pbefore = Pafter
Ha: Pbefore ?‚ Pafter
The alpha level is set at 5 percent (i.e., a = 0.05)
The test statistics of the two-proportions test is the Z-value. For large sample sizes, this Z-value follows the same normal distribution as the well-known standardized z-value for normally distributed data.
The Z-value is calculated as:
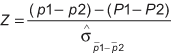
Where (p1 – p2) is the observed difference between the sample proportions, (P1 – P2) is the difference between the population proportions assuming that Ho is true (in this example (P1 – P2) = 0).
is the standard error (SE) of the difference between the two proportions.
Start by finding . It is calculated as:
Where p1 and p2 are the sample proportion use the sample proportions to estimate the standard error because the population proportions are unknown.
Using the data from the example SE is:
Using these results the Z-value is calculated as:
The Z-value of -0.69 is compared with the critical value that must be exceeded to reject the null hypothesis with an alpha risk of 5 percent and can be derived from the Z distribution.
In this case, the sample size is large enough to assume that the Z distribution follows the standardized and normally distributed z distribution. An Alpha risk of 5 percent (or 0.05) corresponds to a critical value of +/-1.96 for a two-tailed test.
Since -0.69 is bigger than -1.96, we have to accept the null hypothesis that the population proportions are the same. The Six Sigma project has not significantly improved the failure rate. Table 1 shows the Minitab output of the same test:
| Table 1: Test and Continuous Improvement (CI) for Two Proportions | |||
| Sample | X | N | Sample p |
| 1 | 9,900 | 10,000 | 0.990000 |
| 2 | 7,928 | 8,000 | 0.991000 |
| Difference = p (1) – p (2); Estimate for difference: -0.001; 95% CI for difference: (-0.00384355, 0.00184355); Test for difference = 0 (versus not = 0): z = -0.69 P-Value = 0.491 |
|||
Summary
Use a two-proportions hypothesis test to determine whether a Six Sigma project actually improved the process. The test compares the percentages of two groups and only works when the raw data behind the percentages is available.
