The precision of a measurement system is commonly assessed using a gage repeatability and reproducibility (GR&R) study.  Part 1 of this article discussed metrics used in measurement system analysis. Here, Part 2 compares commonly used GR&R metrics with probabilities of misclassification.

Comparison of GR&R Metrics with Probability of Misclassification Using Numeric Simulation

A simulation study was undertaken to quantify the relationship between guard banding, percent tolerance (also known as the precision-to-tolerance [P/T] ratio), and the probability of misclassification – all in the presence of varying distributions for both part values and gage error. A response surface designed experiment was utilized to generate a balanced set of factor level combinations. The following four factors were used to summarize the important characteristics of the gage and part distributions:

1. True value capability index, P_pk. This factor describes variance of the true value population with respect to specification limits, including the centering of the true value mean, µ, within the specification limits.

Where CPL = the difference of the center line and the LSL (lower specification limit) and CPU = the difference of the USL (upper specification limit) and the center line:

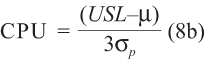
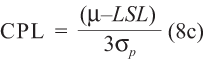
2. The ratio

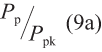
Where P_p is described by equation (9b). This factor describes the “centeredness” of the true value population within the specification limits.

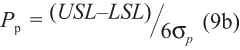
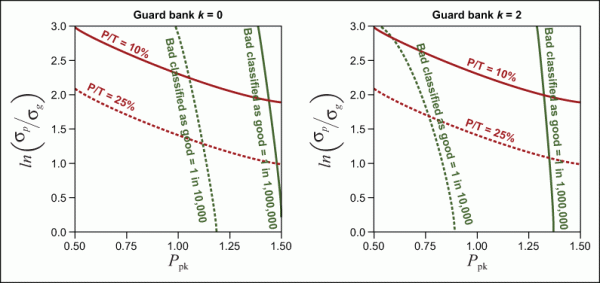
3. The ratio

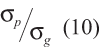
This factor describes gage variance with respect to true value variance. This is effectively the inverse of percent process [see equation (4) in Part 1] divided by 100 percent.

4. Guard band count taken as k, where k (11), is the number of gage standard deviations (σ_g) taken within each specification limit to establish guard banded specifications.

Assuming normal distributions for gage variance and true value populations, each of these four factors can be used to establish probability density functions for gage variability and “true” value population with respect to specification limits, but without having absolute values of gage variance and true value population. (Note: In reality, there is no such thing as a “true” value since GR&R only seeks to understand the precision of the measurements versus some measurement space [either the tolerance or the observed spread of the parts – which also includes the gage variation]. References to a “true” value imply that accuracy was studied but that is not included in this article.)

These probability functions can be used to calculate percent tolerance and probability of misclassification. The four factors can be combined to establish a space of typical gage variance, true value population variance and guard banding, which are then used to map percent tolerance and probability of misclassification over the various combinations of these factors. Once these two gage metrics are mapped over combinations of these factors, relationships between the two metrics can be established over the same space. If a 1-sided specification equation is not available, however, the same probability distribution functions can be established and the same mapping is still possible.

These four factors are not independent from one another, and when combined to map and compare gage metrics they will not form an orthogonal comparison grid, where grid lines are perpendicular to intersection. However, comparison between gage metrics over ranges of each factor provides a means to draw general conclusions about the effectiveness of each metric in various circumstances without having absolute measured values. The lack of orthogonality must be taken into account when making this comparison, but it does not preclude obtaining some useful information as a result of the study.

Percent tolerance and probability of misclassification can be modeled over combinations of the four factors using response surface analysis, in which models can be represented using contour plots of the fitted surfaces. The type of response surface design of experiment (DOE) chosen for study is a central composite design (CCD).¹ In this type of design, factorial combinations of factors – along with center points and axial points – are used to structure study inputs. The resulting data can be used to fit models involving primary factors, their interactions and second order polynomial terms. The ratio defined in (10) can vary over multiple orders of magnitude; for this simulation the input was converted to a natural log scale that forced a range over multiple orders of magnitude to be input on a linear scale. Experimental results can be used to estimate multifactor regression equations, which can then be used to numerically predict responses over the design space.

The design space is chosen to represent typical ranges of equations (8), (9), (10) and (11), while avoiding conditions where combinations of (10) and (11) would satisfy (7), thereby resulting in null values for probability of misclassification. The values of axial points are selected as 1.1 times larger than the extent of primary factorial points away from the center point for similar reasons. The lower axial point for (11) is set to zero to avoid a negative value. The values of the factorial points, center points and axial points for the three remaining inputs to the design are shown in Table 1.

Table 1: DOE Inputs for Response Surface Mapping Percent Tolerance and Probability of Misclassification
Factor	Center	Factorial Lower, Upper	Axial Lower, Upper
Ppk / Pp	1.0	0.5, 1.0	0.45
Ppk	1.0	0.5, 1.5	0.45, 1.55
	1.5	0, 3	-0.15, 3.15
Guard band k	1.0	0, 2	0, 2.1

Given a value for each of the four factors and known specification limits, the values of process mean, gage variance and process variance can be calculated. From here, percent tolerance and probability of misclassification can be estimated. An LSL of zero and USL of 100 were used to numerically simulate probability distribution functions for gage variance and true value population based on combinations of equations (8a), (9a) and the natural log of (10). These probability distribution functions were used to calculate percent tolerance according to equation (5) and to estimate the probability of misclassifying a bad unit as good and a good unit as bad for each combination of the four factors in the CCD DOE. All outputs were found to vary over more than 2 orders of magnitude and, as a result, the outputs were analyzed using a natural log scale to simplify analysis. (Population simulation, probability of misclassification estimation and CCD DOE analysis were done with Minitab v16.)

The DOE analysis of variance (ANOVA) table provides information regarding significant terms and lack-of-fit for each of the outputs studied. Significant terms are taken as having a p value less than 0.05.¹ The predicted R² is chosen to determine lack-of-fit and usefulness of the model to predict results. Predicted R² captures the percentage of a response variation explained by relationships with inputs using predicted model output versus observed output to quantify lack of fit. The second order polynomial term for (9a) was found to be significant to the probability of good observed bad and percent tolerance. The influence of (9a) on percent tolerance is due to non-orthogonality of input factors. Based on observation of insignificant first order terms and interaction terms for (9a), the DOE input factors were reduced and interaction terms including (9a) were removed. The first order and second order term associated with (9a) were left in subsequent analysis due to the significance of the second order term in the model for probability of good observed bad. Goodness of model fit and factor significance for each of the three measurement system analysis metrics using the reduced model terms are shown in Table 2.

Table 2: Goodness of Model Fit and Factor Significance
	Bad Observed as Good	Good Observed as Bad	Percentage Tolerance
R% predicted	97.4	98.44	99.99
	p-values
Constant	0.166	0.001	0
Ppk	0.68	0.008	0
Ppk / Pp	1	1	1
	0.005	0	0
Guard Band k	0	0.068	0.024
Ppk * Ppk	0	0	0
Ppk / Pk * Ppk / Pk	0.057	0.002	0
*	0.67	0	0.01
Guard Band k * Guard Band k	0.188	0.491	0.01
Ppk *	0.007	0	1
Ppk * Guard Band k	0	0	1
* Guard Band k	0.028	0.109	1

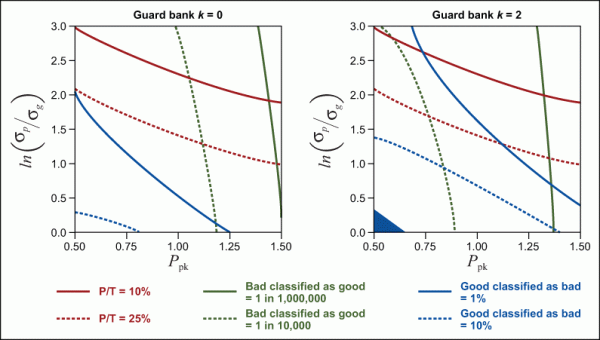
Response surface contour plots for the P/T ratio and the probability of bad misclassified as good are overlaid in Figure 4 over the studied range of  and P_pk. Two overlaid contour plots are drawn for guard band k = 0 and 2 respectively. Both plots have a fixed value P_pk  ⁄  P_p = 1.

The bands defined by the adjacent contour lines indicate sensitivity of each output to the input factors on each axis. The probability of misclassifying bad as good shows the most sensitivity to P_pk and is relatively insensitive to . The opposite is true for P/T ratio. This trend holds true for both plots at two different guard band values. This sensitivity analysis establishes that the probability of misclassification is more dependent on the probability that a value is bad or good, as opposed to the probability that the measured value is different from the true value. Curvature is shown in the P/T ratio response, which indicates sensitivity to P_pk and ; this curvature is due to non-orthogonally of the input factors. According to equation (5), the P/T ratio is not dependent on process standard deviation – and is only dependent on process mean for one-sided specifications. In this model, however, gage standard deviation is established based on a ratio with process standard deviation, and process standard deviation is an input to the factors on each plot axis.

The influence of guard banding on each of the two outputs is established by comparing the two plots in Figure 4. P/T ratio does not change as a function of guard banding, which is expected according to equation (5). The probability of misclassifying bad as good changes such that the probability is reduced for lower values of process capability. Guard banding has more influence on the probability of misclassifying bad as good when the probability is greater than 1 in 1,000,000; for values equal to or less than this level, guard banding has a smaller influence on reducing the probability of misclassification (i.e., at a higher process capability).

The difference in sensitivity of each output over the plot range at both values of guard banding illustrates four conditions for gage precision, as defined by P/T ratio, and probability of misclassification. They are:

• Condition 1: 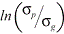 > 2.0, P_pk > 1.3

P/T ratio is within typical acceptance limits and the probability of misclassifying bad as good is relatively small.

• Condition 2: 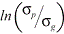 < 2.0, P_pk > 1.3

P/T ratio is larger than typical acceptance limits; however, the probability of misclassifying bad as good is relatively small.

• Condition 3: 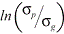 < 2.0, P_pk < 1.3

P/T ratio is larger than typical acceptance limits and the probability of misclassifying bad as good is relatively large.

• Condition 4: 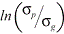 > 2.0, P_pk < 1.3

P/T ratio is within typical acceptance limits and the probability of misclassifying bad as good is relatively large.

For conditions 1 and 3, the P/T ratio and probability of misclassifying bad as good agree in their assessment of gage suitability for decision making. In condition 1, the gage is generally considered suitable. In condition 3 the gage is generally considered ill-suited for decision making. For conditions 2 and 4, the P/T ratio and probability of misclassifying bad and good disagree in their assessment of gage suitability for decision making. In condition 2, the gage is considered imprecise; however, the underlying true value population is sufficiently far away from specification values as to minimize the probability of misclassifying bad as good. This condition may avoid risk of false acceptance by misclassifying non-conforming values as good, but additional cost may reside in the probability of misclassifying good as bad. In condition 4, the gage is considered precise, but the underlying true value population is close enough to specification values such that the probability of misclassifying bad values as good remains high. Here the gage may be precise enough to differentiate values within the specification tolerance, but the magnitude of measurement error is still large enough to warrant significant risk in using the measurement system to sort values, where the sort condition is based on specification limits.

Guard banding reduces the probability of misclassifying bad as good, thereby increasing the suitability of a measurement system for making effective decisions at lower values of process capability. The probability of misclassifying bad as good is not reduced to zero over the entire range of P_pk shown. Even for guard banding at 2σ_g, the probability of misclassifying bad as good can remain relatively high at low process capability.

Guard banding has been shown to increase the probability of misclassifying good as bad. This is illustrated in Figure 5 in which response surface contour plots for the probability of good misclassified as bad are overlaid with the same contours shown in Figure 4. Plot ranges of and P_pk are the same as in Figure 4. Two overlaid contour plots are drawn for guard band k = 0 and 2, respectively. Both plots have a fixed value P_pk  ⁄  P_p = 1.

As in Figure 4, the bands defined by the adjacent contour lines indicate sensitivity of each output to the input factors on each axis. The probability of misclassifying good as bad is nearly equally sensitive to P_pk and ; probability of misclassifying good as bad increases as P_pk or decrease. The influence of guard banding on the probability of misclassifying good as bad is seen by comparing the two plots in Figure 5. When no guard banding is applied, the probability of misclassifying good as bad is less than 1 percent over the range of P_pk and , where P/T and the probability of misclassifying bad as good would be considered generally acceptable. When guard banding is applied, the probability of misclassifying good as bad is found to increase at lower values of P_pk and . For extremely low values of P_pk and shown in the plot, guard banding is shown to satisfy the condition defined by equation (7); the result indicates that all values would be classified as bad. Comparing the two probabilities of misclassification illustrates that as guard banding is applied, the probability of bad misclassified as good will decrease, but the probability of good misclassified as bad will increase. This tradeoff is most prevalent at low values of P_pk and .

The four conditions previously established can be summarized to include information on the probability of misclassifying good as bad.

	Ppk < 1.3	Ppk > 1.3
> 2.0	Condition 4 The P/T ratio is within typical acceptance limits The probabilities of misclassification are relatively large.	Condition 1 The P/T ratio is within typical acceptance limits. The probabilities of misclassification are relatively small.
< 2.0	Condition 3 The P/T ratio is larger than the typical 30 percent acceptance limits. The probabilities of misclassification are relatively large.	Condition 2 The P/T ratio is larger than the typical 30 percent acceptance limits. The probability of misclassifying bad as good is relatively small and the probability of misclassifying good as bad is relatively large.

For conditions 1 and 3, the P/T ratio and probabilities of misclassification agree in their assessment of gage suitability for decision making. Based on this analysis, a gage is suited for decision making in condition 1. For condition 2, the imprecision of the gage does not jeopardize the risk of false acceptance. A significant risk of false reject (i.e., excess scrap), however, may exist, and the gage’s suitability for decision making is conditional based on the circumstances surrounding the measurement. For condition 4, the gage’s precision may not effectively eliminate the risk of misclassifying good values as bad or bad values as good; the gage may not be considered suitable for applications of sorting values within a population where the sorting condition is based on specification limits.

Non-normal Distributions

The aforementioned DOE simulation approach and results are based on normal distribution assumptions for underlying true value populations and gage error. Although gage error typically follows a normal distribution, underlying true value populations may not be. Typical GR&R results should be relatively insensitive to non-normal data sets, where the probability of misclassification will be sensitive.

Lognormal true value populations and any true value population with significant skew will not have symmetric probability density functions about the distribution arithmetic mean. As a result, these DOE simulations cannot be generalized based on the exact same factors; results need to be based on absolute distribution position relative to specification values. Initial attempts to repeat this trial using non-normal distributions suggest general agreement with these results, except that the results are dependent on the absolute position of the population within the specification limits.

Conclusions

Comparison of GR&R metrics, namely P/T ratio, with the probabilities of misclassification reveals that precise measurement systems may still generate results with significant probabilities of misclassification. A DOE study using numeric simulation revealed that the most significant risk of misclassifying measured values exists when a gage is considered precise with respect to specification tolerance, but the population of values being measured resides near or outside of specification tolerance. Where true value population is defined by a P_pk capability metric less than 0.75, a gage may be classified as suitable with a P/T ratio less than 10 percent, while probabilities of misclassifying good values as bad or bad values as good may be greater than 1 in 10,000.

Guard banding influences probabilities of misclassification, and can be used to reduce the probability of misclassifying bad values as good at the cost of increasing the probability of misclassifying good values as bad. Guard banding has the most influence on probability of misclassification for imprecise measurement systems and when a population of values being measured has low capability index.²

References

1. Montgomery, D. C., and G. C. Runger. “Gage Capability and Designed Experiments Part II: Experimental Design MEthods and Variance Component Estimation.” Quality Engineering 6 (1993b): 289-305.
2. Taylor, Wayne. “Generic SOP – Statistical Methods for Measurement System Variation, Appendix B Gage R&R Study.” Wayne Taylor Engerprises, Inc., n.d