
As a customer, the worst experience I can imagine is being a casualty of process variation. ‘It doesn’t seem that bad,’ you may be thinking to yourself. Just remember back to the last time you:
- Went grocery shopping only to select the slowest teller in the store.
- Received a haircut that was shorter or longer than usual, and definitely not what you asked for.
- Decided to go shoe shopping, but got stuck with the most ignorant salesperson available.
You can probably come up with a short list of your own experiences without thinking too hard, but you can also probably remember picking the fastest line in the grocery store, receiving a perfect haircut and being ecstatic with your salesperson’s knowledge. That was a great feeling, wasn’t it?
Let’s examine a few ways to help us evaluate variation in processes. First, it’s important to put yourself in the right frame of mind – imagine that your children have been whining for pizza all day, and on your way home you stop by your local pizza parlor to order a pizza that you (and your kids) are waiting for. Consider the general concept of variation by examining the preparation time (in minutes) of 10 pizzas being prepared by your two local pie shops. The times are listed below.
| ABC Pizzeria | ||||||||||
| XYZ Pizza To Go |
If we use common statistical tools, such as mean, median, mode and midrange, we get the following results:
| Mean | ||
| Mode | ||
| Midrange |
You can see from these results that the two pizza parlors have the same measures of central tendency, so, on average, customers wait the same amount of time for pizzas at the two restaurants. Based on these measurements alone, we cannot see any distinguishable difference between the two processes.
If we return to the original data points, however, we can see a very distinguishable difference: ABC Pizza has preparation times with much less variation than the times for XYZ Pizza. If all other characteristics of the pizza (taste, temperature, size, topping quality, service friendliness, etc.) are equal, customers are likely to prefer the ABC Pizza where they will not become annoyed by being the one person whose pizza preparation time is much slower than the others.
By inspecting and comparing the differences in variation between the preparation times of the two pizza companies, we can get a sense for the variation. But in business, we need more than a sense – we need to measure and quantify the process variation. For this reason, we are going to display the use of two tools: range and standard deviation.
Use the Range to Understand your Process Variation
The easiest way to measure variation is the range. It is simply the difference between the highest value and the lowest value.
For the ABC Pizza data, the range is the difference between 7.7 minutes and 6.5 minutes, which is 1.2 minutes. The range for XYZ Pizza preparation time is 10.0 – 4.2 = 5.8 minutes. This much larger range of data suggests that the XYZ Pizza process has a greater amount of associated variation.
Although the range is very easy to compute, it also has some drawbacks. It is often inferior to other measures of variation that use the value of every score. For instance, if we look at two groups of data, A and B found in the table below, we can compute the ranges to be 19 and 16, respectively. This analysis would suggest that group B has much less variation than group A, even though group A scores are very close together while group B scores have more variation.
| Group A | Group B |
|---|---|
| 1 | 2 |
| 20 | 3 |
| 20 | 4 |
| 20 | 5 |
| 20 | 6 |
| 20 | 9 |
| 20 | 11 |
| 20 | 14 |
| 20 | 18 |
| Range = 19 | Range = 16 |
The range may be misleading in this case because it only uses the maximum and minimum data set values. Standard deviation would be a better tools for variation in this case.
You can see from these results that the two pizza parlors have the same measures of central tendency, so, on average, customers wait the same amount of time for pizzas at the two restaurants. Based on these measurements alone, we cannot see any distinguishable difference between the two processes.
Use Standard Deviation to Understand your Process Variation
One of the most important measures of variation is the standard deviation. The standard deviation (s) of a set of sample scores is a measure of variation of scores about the mean, and is defined by the following formula:
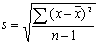
Using this formula we can now compare the variation of the two pizza companies and note that the standard deviation for ABC Pizza (0.48 minutes) is much lower than the standard deviation for XYZ Pizza (1.82 minutes). This supports our original observation of the data and our results of the range as a quantification of the variation.
In our definition of standard deviation, we referred to the standard deviation of sample data as s. If we want to calculate the standard deviation (![]() ) of a population, we would divide by the population size N, instead of n-1.
) of a population, we would divide by the population size N, instead of n-1.
![]()
The range may be misleading in this case because it only uses the maximum and minimum data set values. Standard deviation would be a better tools for variation in this case.
You can see from these results that the two pizza parlors have the same measures of central tendency, so, on average, customers wait the same amount of time for pizzas at the two restaurants. Based on these measurements alone, we cannot see any distinguishable difference between the two processes.