Tag: standard deviation

Understanding Process Sigma Level
Updated:Six Sigma is a data-driven approach to quality, aimed at reducing variation and the associated defects, wastes and risks in any process. This article explores the basics of Six Sigma process quality – definition and measurement. In a set of data, mean (μ) and standard deviation (σ) are defined as: μ = x1 + x2 […]
Read more »
A Study of Estimates of Sigma in Small Sample Sizes
Updated:This paper looks at some of the methods of estimating standard deviation (which I will usually refer to as ‘sigma’). Additionally, I propose a new formula for estimating sigma for small sample sizes and also present a means to mathematically evaluate these competing estimates of sigma. The question was posed to me: “I have five […]
Read more »
Getting the Most out of a Capability Analysis
Published:The process capability indices Pp and Cp describe how closely a process can operate within its specification limits. Many articles describe the difference between Pp and Cp simply: one is short term, one is long term. Moving beyond such a description, this article focuses on the untapped power of capability analysis and shows you how […]
Read more »
Calculating Call Center Interarrival and Service Times
Published:Two Six Sigma professionals recently posed questions in the iSixSigma Discussion Forum relating to queuing theory in a call center. One reader wanted to know how to calculate average and standard deviation for service time and interarrival time – the amount of time between the arrival of one customer and the arrival of the next. […]
Read more »
Variation – The Root of All Process Evil
Published:As a customer, the worst experience I can imagine is being a casualty of process variation. ‘It doesn’t seem that bad,’ you may be thinking to yourself. Just remember back to the last time you: Went grocery shopping only to select the slowest teller in the store. Received a haircut that was shorter or longer […]
Read more »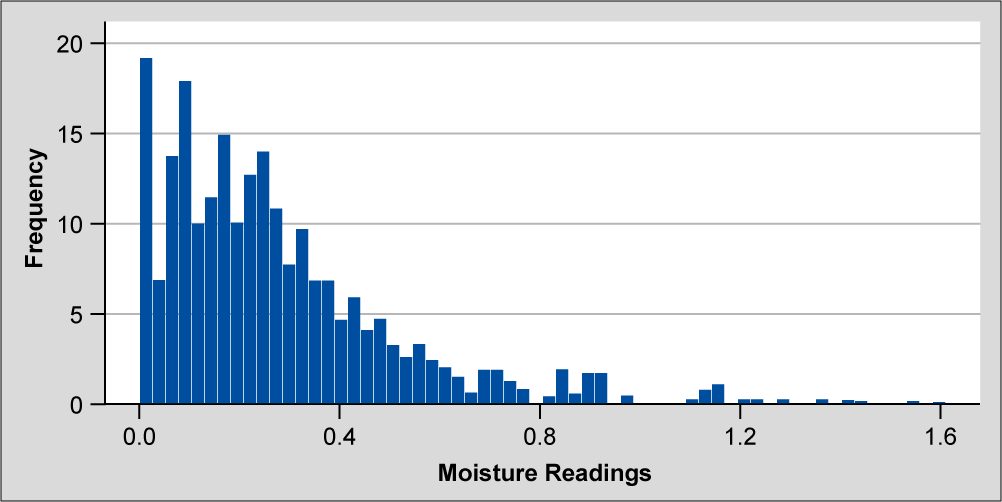
Estimation Method Helps Analysis of Truncated Data Sets
Published:A data set with a physical limit – such as time, which has a lower bound of zero – often cannot be transformed using the usual tools for non-normal data. To determine process capability and perform further statistical analysis, use the standard deviation calculated as if the data were not truncated, along with a correction factor.
Read more »