
CoV is a simple calculation to measure the variation in your process. Let’s see how to do the calculation, explore an industry application, and answer a few questions about CoV.
Overview: What is the coefficient of variation (CoV)?
CoV, also known as the relative standard deviation, is a dimensionless measure of relative variability. It is the ratio of the standard deviation and mean of your data set. The formula is:
![]()
Graphically, this can be seen below. Note that the two means are equal, but the two standard deviations are different. The larger standard deviation has a CoV of 0.03, or 3%, while the smaller standard deviation results in a CoV of 0.025, or 2.5%.
Visually, the curve with less variation has the smaller CoV. This is interpreted as meaning the dispersion of points around the mean is less for the blue curve than for the dashed red curve. Less variation in your process is preferred.
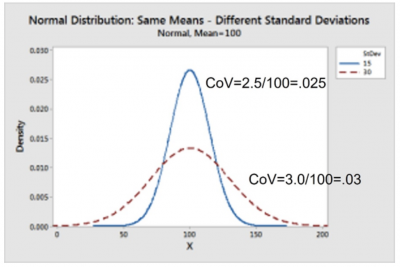
Comparing coefficient of variation
An industry example of the coefficient of variation
A customer call center was evaluating the performance of two of their associate teams with respect to the time they spend on a customer call. Data was collected, and the mean and standard deviation of call time were calculated.
The call center manager decided to calculate the coefficient of variation to compare the two teams. While the average call time was close (4.5 minutes vs. 4.3) one team had a standard deviation of 1.5 minutes, while the other was 2.75 minutes, respectively. This resulted in a CoV of 33.33% vs. 64%.
The manager formed an improvement team to try to find the root cause why one team had a relative variability almost double the other team. The root cause was found to be a result of training, tenure and supervisor. Changes were made, and both teams then performed with minimal call length variation.
Frequently Asked Questions (FAQ) about coefficient of variation
1. What is considered a good level for the coefficient of variation?
Many people believe a CV<10% is very good, 10%-20% is good, 20%-30% is acceptable, and CV>30% is not acceptable.
2. What is the advantage of using the coefficient of variation over the standard deviation?
The CoV is a relative measure of variation against the mean. It is unit-less. so different data sets can be easily compared. This cannot be done with the standard deviation or variance.
3. What are the differences between the coefficient of variation and the standard deviation?
Here is a table showing the difference:
