
Does your data appear to be normally distributed? If so, the empirical rule will allow you to understand approximately how your data is distributed. This will allow you to calculate probabilities and percentages for various outcomes. Let’s learn more.
Overview: What is the empirical rule?
Before you can fully understand the empirical rule, you need to understand something about the normal distribution. The normal distribution is a hypothetical construct developed by Johann Carl Friedrich Gauss, a German mathematician and physicist.
The normal distribution, also known as the Gaussian distribution, is a probability distribution with the following properties:
- defined by the mean and standard deviation
- is symmetrical around the mean
- distributed such that the data near the mean is more frequent than in the tails
- has a bell shaped appearance
- the mean, median and mode are the same
The formula for the normal distribution is:
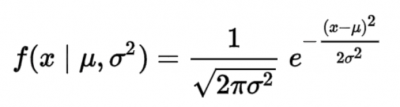
Now that you understand the normal distribution, let’s see how the empirical rule fits in. The word “empirical” comes from the concept of empirical research. This type of research relies on observations and measurements of real-world outcomes rather than pure theory.
Gauss observed that data from many common applications seemed to follow a certain distribution. This gave rise to an approximation of how the data values would be distributed based on the mean and standard deviation of continuous data.
According to the empirical rule, if you add and subtract the value of one standard deviation to the mean, you should encompass approximately 68% of your data. Adding and subtracting two standard deviations will encompass approximately 95%, and with three standard deviations, you will now have approximately 99% of the data. Notice, we said approximately. If you actually use the probability function, you will get more exact percentages.
The actual values for one, two, and three standard deviations are: 68.2689%, 95.45%, and 99.73%.
An industry example of the empirical rule
A Six Sigma Black Belt collected some data on turnaround time for processing invoices. She calculated the mean turnaround time to be 38 minutes with a standard deviation of 12 minutes. Her manager wanted to know the probability was of taking more than 60 minutes to process an invoice. Using the Excel function Normdist, she was able to calculate the probability of exceeding a processing time of 60 minutes to be 3.3377%.
To confirm this, the values were converted to the number of standard deviations that 60 minutes was away from the mean. This computed to 1.83333. Using the Excel Normsdist function, the probability was calculated to be 3.3377%, the same as above.
Frequently Asked Questions (FAQ) about the empirical rule
1. What is the empirical rule?
It is an approximation of the distribution of values assuming a normal distribution. According to the empirical rule, approximately 68% of your data should be between your mean, plus and minus one standard deviation. For two standard deviations, it will be approximately 95%, and for three, it will be approximately 99%.
2. What is the empirical rule used for?
It will allow you to estimate probabilities and percentages for various outcomes.
3. Can I use Excel to calculate the probabilities of the empirical rule?
Yes. You can use the Normsdist() function, where you would enter the number of standard deviations in the parentheses.