
The transfer function has a number of uses in Lean Six Sigma (LSS). While the statistical and mathematical explanation requires in-depth use of higher-order math and statistics, our focus will be on a simpler explanation and its application rather than its derivation.
Overview: What is Y=f(X)?
Y=f(X) is one of many types of transfer functions. In a nutshell, a transfer function, as defined by Mathworks, is a “convenient way to represent a linear, time-invariant system in terms of its input-output relationship.”
Most of us are probably comfortable with the terms linear, input, and output. But, what does “time-invariant” mean? It means the value and effect of the variable does not change across time. For example, the effect of temperature on your output would be the same at time period 1 as it would at time period 5.
In LSS, the term Y=f(X) is spoken as “your output is a function of your input.” It’s that simple. To improve your process, you can’t focus on changing your output. You must identify the critical inputs and then improve them since your output is a function or outcome of those inputs.
The tricky part is identifying those critical inputs. In the DMAIC methodology, the purpose of the A, or analyze, phase is to identify the root causes or critical inputs. That is what you will improve in the I phase.
For example, in simple linear regression, the transfer function below is used to describe the linear relationship between your output or dependent variable and single input or independent variable:
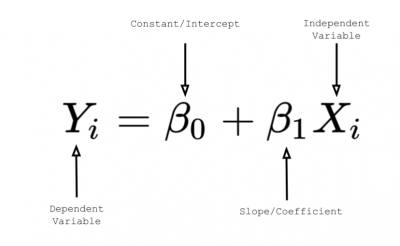
Image source: towardsdatascience.com.
In multiple regression, use the following formula to describe the relationship between your output or dependent variable Y and multiple input (independent or predictor) variables X.
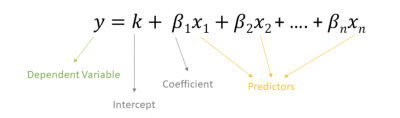
Image source: www.superheuristics.com.
3 benefits of Y=f(X)
When it comes to representing relationships, it’s best to KISS (keep it simple and specific).
1. Simplicity
Modeling a system can become complex. If you keep the notation simple, most people will be able to understand the principle and what you are trying to represent.
2. States the obvious
Your outputs are a function of your inputs — it’s a simple concept. To change your outputs, you must identify the critical inputs that have the best correlation and possible causation with the output.
3. If your inputs are known, you can determine your output
Since the transfer function is a simple mathematical relationship, you can compute the value of your output if you know the value of your input(s).
Why is Y=f(X) important to understand?
Despite its simplicity, the Y=f(X) relationship has some intricacies you need to understand.
Use in linear systems
The transfer function is defined only for linear time-invariant systems. For nonlinear systems, you use a time domain system where the effect of the input varies over time.
Use meaningful inputs
If you include inputs that are not statistically significant, your predicted output may not be accurate and your prediction model not representative of your system.
Can be used for discrete as well as continuous systems
If your input consists of both variable and discrete variables, you can still write a transfer function. This is often the case in regression, where your independent variables are both variable (time) and discrete (counts).
An industry example of Y=f(X)
A popular fitness center company was developing a new pitch to sign up new customers looking to get in shape and lose weight. Rather than rely on age-old hyperbole and generic statements, the owner decided to use a more scientific approach. He had read about the concept of a transfer function described by Y=f(X) and wondered if it could be used for his situation.
He decided to start simple and use weight loss as his Y since it was easily measurable. He tried to identify key X inputs, remembering that weight loss doesn’t happen on its own but is a function of certain activities his clients will engage in. He and his team came up with caloric consumption, hours of exercise, type of exercise, number of previous diets, self motivation score, and personal assessment of body image.
Using the Y=f(X) relationship, the owner was able to establish a model for predicting the success of a client to achieve their weight loss goals.
3 best practices when thinking about Y=f(X)
Let’s cover a few things to think about when you are dealing with transfer functions.
1. Select meaningful Xes, or inputs
Adding meaningless Xes to your transfer function does not add to the accuracy of your Y. Be sure you have identified the ones that are statistically significant.
2. Confirm your accuracy
Be sure to calculate the accuracy of your model and confirm that all assumptions for validity have been met. Not only do you want to understand the correlation between your Xes and Y, you will also want to understand the sensitivity of your Y to varying levels of X.
3. Test your model
Before you utilize your model for prediction, do some confirmatory assessments to be sure it will model what you want to the degree of accuracy you need.
Frequently Asked Questions (FAQ) about Y=f(X)
1. In words, what does Y=f(X) mean?
When vocalized, this phrase says that your output is a function of your input(s). To make a change in the output of your process, you will need to identify and change the inputs.
2. What is the purpose of a transfer function?
It’s a simple way to represent and define the relationship of the inputs and outputs of your linear time-invariant system.
3. Can I use Y=f(X) for a nonlinear system?
Except for some rare instances, the transfer function, Y=f(X), is defined only for a linear relationship.
Summarizing Y=f(X)
The transfer function Y=f(X) is a simple and convenient way to model the relationship between a system’s inputs and its outputs. The Y, or output, is a function of the X(es), or inputs. To improve the outputs, you must identify the key inputs and change them.