Key Points
- Verification is the process of guaranteeing a model is producing the right outcomes.
- Validation is the process of making sure a model is representative of real-world conditions.
- Both are useful when running models to check for errors or predict outcomes.
Many people use the terms verification and validation interchangeably without realizing the difference between the two. Not understanding that difference can lead to many models that do not truly represent a real-world process and lead to errors in forecasting or predicting the outcomes. In this article, we will explore the meaning, importance, differences, and basic methods of verification and validation.
What Is a Model?
©Oakland Images/Shutterstock.com
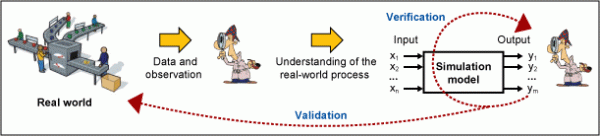
The first step to understanding these two different processes is to understand what a model is. A model, whether it is a mathematical, simulation, or physical model is a representation of a real-world process. The model can be used for studying, experimenting, or making a prediction of a real-world event. You don’t need to directly observe or make changes to the real-world process.
A model is created to understand relationships among independent variables or inputs (Xs) and the dependent variable or the outcome (Ys). Examples of mathematical models well-known in the Lean Six Sigma (LSS) world are Little’s Law and other queuing models.
Simulation models can be built using computer software. A physical model is not common to Lean applications. However, it is frequently used for experimental purposes in engineering, architectural, and science applications.
British statistician George E.P. Box said, “Essentially, all models are wrong, but some are useful,” which reminds the practitioner that neither is a model the real-world process nor can that process be fully represented. The question of how good a model can be is answered using verification and validation.
The first pitfall that many LSS practitioners fall into is using the model that they created without both verifying and validating it. The second pitfall is that they go through one and assume that’s all that’s necessary. This leads to unrealistic predictions, misguided results, and a loss of the integrity of the model.
What Is Verification?
Verification is the process that ensures that the model is producing or predicting the right outcomes based on the relationships of input variables and output variables that are built into the model. The verification process does not rely on, or compare to, the real-world process.
Its purpose is to confirm that the model is doing exactly what the modeler “thinks” it should do when it was created. If it is desirable for the model to return a rounded-up integer value of X1 divided by X2, does the model always provide the integer result of 1 when X1 = 3 and X2 = 4 is entered? Or does it return a result of 0.75?
What Is Validation?
Validation is the process to ensure that the model is representing the real world as much as possible. The validation process helps a modeler be certain the correct model is built. It relies heavily on the data collected from the real world, and the perception and understanding of the process of the modeler. The validation process ensures that the model is doing what the real process is doing. (See Figure 1.)
Testing for Success
Models are just a natural part of any sort of data collection process. You don’t want to start gathering data points to analyze live from production. As such, it makes sense to implement modeling while verifying and validating things from the onset. It’ll keep things running smoothly as you look to implement changes later on.
Example: Ice Cream Stand
Consider a modeler building a model to represent a queuing system at an ice cream stand. He observes the arrival profile of customers and the service rate of the server. Further, he finds that the server serves each customer at a constant rate of three minutes per customer.
He builds a model to predict the waiting time (W) when a customer arrives at the stand and finds that there are customers (X) waiting in the system. He decides to use a mathematical model of W = 3X.
The modeler verifies that he built the model correctly by entering X = 1, 2, 5, 10, and 20 into his equation; the model returns the values of W as 3, 6, 15, 30, and 60 minutes respectively. In this verification process, the model calculates the result correctly based on the modeler’s perception of the linear relationship between W and X.
To validate this model, the modeler would conduct a time study when a customer, Jessica, arrives at the stand. For five different instances, the modeler observes there are 1, 2, 5, 10, and 20 customers in the line. The real system may return different waiting times for Jessica since some customers who are already in the line may decide to leave when the waiting time exceeds their tolerance limits.
As a result, Jessica’s actual waiting time becomes shorter and thus does not consistently follow the linear relationship of W = 3X. In this case, even though the model passed the verification process, it does not represent the behavior of the real system and fails the validation process.
Example: Distribution Center
Why are both verification and validation of a model needed? Consider another example of a process creating a simulation model for a distribution center consisting of four product-sorting machines. Figure 2 shows the schematic of the distribution center.
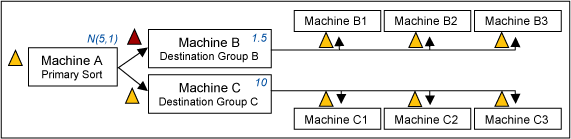
An LSS team collects data on cycle time and processing steps at each machine. After that, the team builds a model using simulation software. Based on the data that was collected and statistically analyzed, the team found that the processing time of Machine A is normally distributed with a mean of 5 minutes and a standard deviation of 1 minute.
Machine B has a constant processing time of 1.5 minutes and Machine C has a constant processing time of ten minutes. Products B and C arrive with equal distribution at Machine A every 5 minutes.
After the model was created, the team ran the model until reaching a steady state and found that there was an excessive queue in front of Machine B, but none in front of Machine C.
Putting It Together
Based on the assumption of the processing time at these three machines, and the arrival profile of products B and C, the team realizes that there could be an error in the model code or parameters. The team ensures that all parameters have been entered correctly.
Eventually, the team found a mistake in the processing time parameter at Machine B – 15 minutes was entered instead of 1.5 minutes. This error-checking process is a verification process. By ensuring that the model is producing what it should be producing, the modeler verifies that the model is error-free.
Consider the same distribution center and a corrected model. The team decides to use the model to predict the behavior of the process during a peak demand period. The team may use data from the previous peak period (such as work in progress, queue length, and queue time from the last known period). They can use the known data as input variables and compare the results of output variables to the last known data collected to adjust the model.
Verification, Then Validation
The validation process should be performed after the verification process has been completed. The validation process normally involves real data, which can consume more of a team’s resources than the verification process. The table below suggests some validation methods for each modeling scenario.
| Modeling Scenarios With Corresponding Validation Methods | |
| Modeling Scenario | Validation Method |
| Model of an existing process, data is available | Test the model in several different cases during the normal and extreme periods using the last known data and compare the model outputs to the last known outcomes |
| Model of an existing process, data is NOT available | Observe the behavior of the real-world process and compare that to the behavior of the model |
| Model of nonexisting process, relationships of variables are known | Use correlation analysis to analyze the relationship between the outcome of the model and the input variables. Compare that to the known relationship of the variables. |
Other Useful Tools and Concepts
Running simulations can be complex, especially when you consider all the factors at play. However, you can take a closer look at your yield when looking at single-use reliability modeling. This approach isn’t perfect for predicting the future, but it’s far closer than other types of modeling.
Additionally, you might want to look into the Monte Carlo simulation. This modeling methodology is used for managing risk, a consideration any team lead is going to have to keep in mind. By utilizing this approach, however, you can make sure everything is accounted for when production is live.
Final Thoughts
No one verification or validation process fits all scenarios. A modeler should be aware of the available methods. Both verification and validation processes should be completed at the earliest stage in the project – and as thoroughly as possible. The key question for verification is whether the model was built correctly. After verification, the model should be error-free. The key question for validation, on the other hand, is whether the correct model was built. After validation, it should be clear that the model acts similarly to the real-world process so a team can be confident in using it to predict the behaviors of a process.
