
Let’s look at the financial division of a global conglomerate. One of its businesses was providing loans to corporate clients. Although a dominant player in the market, the company still had to compete with other organizations to provide financing and lending to myriad businesses. By using binary logistic regression to help refine its lending offers, the company increased its business by 9.8%.
Let’s learn more about how that was accomplished.
The company’s win ratio for loan bids was decreasing, and its profitability of loans was declining
As a major player in the corporate lending marketplace, this company had a long history of success in placing loans with major corporate clients. Recently, more companies had entered the loan business and were winning more frequently.
The business model was relatively simple. Companies seeking business loans would solicit bids from several competitors who would evaluate the conditions of the loan and submit a sealed bid to the company by a certain date. Since the bids were sealed, the company didn’t know ahead of time whether their bid was competitive or whether they had won or not until the bids were opened and the winning company announced.
The company in this story noticed its win ratio had been declining for the past 9 months and decided to put a team together to evaluate why this may be happening. They also noted when they won a bid, the profitability was lower than historical levels. They sensed they were leaving money on the table, and although they were winning bids, they may have been pricing the loans too low.
Since this company was a leader in deploying Six Sigma, they included one of their Master Black Belts (MBB) on the team looking for root causes for the decline in the loan win ratio and profitability. Some of the key independent variables of the loan process were the interest rate, term length, risk, desired rate of return, points, estimated rate of inflation, size of loan, and credit worthiness of the client.
A team of loan experts would evaluate the bid request and determine whether the company wanted to bid for the loan and, if so, what would be the cost to the client.
They used binary logistic regression to evaluate the probability of winning the bid
As the name implies, binary logistic regression, in this context, is a special case of multiple regression.
In a traditional multiple regression, the independent, or X variables can be either continuous data or discrete data with the response, or Y variable being a continuous value. In many cases, the relationship between the independent and dependent or response variables is linear. Based on the historical values of the paired data of independent and dependent variables the purpose of multiple regression is to predict some continuous value for Y based on values for the Xs.
While binary logistic regression also makes use of X variables, the Y, or response variable is the probability of one of two possible or binary occurences.
In our story, the company either won the bid or they didn’t win. Those are the only two possible outcomes. Saying they almost won or barely lost are irrelevant statements. They won or they didn’t. The calculations can be set up to predict the probability of winning or losing.
For example, if you wish to predict the probability of winning, say 80%, the probability of losing would be 100%-80%, or 20%. By changing the values of the independent variables, you will either increase, decrease, or have no impact on the probability of your outcome.
While the traditional regression assumes a linear relationship, the binary logistic regression assumes a logistic relationship, which is S-shaped rather than a straight line.
Below is a comparison of the shape of a linear and logistic curve assuming a single binary Y output and a single X input. Notice the linear model can theoretically go above 100% or below 0%. Obviously that isn’t feasible.
On the other hand the logistic curve has a maximum probability of 100% and a minimum of 0%. Once the curve is drawn, you can physically select any value on the X axis, go up to the curve, and read across to the left to determine the probability of the outcome given the value for that X.
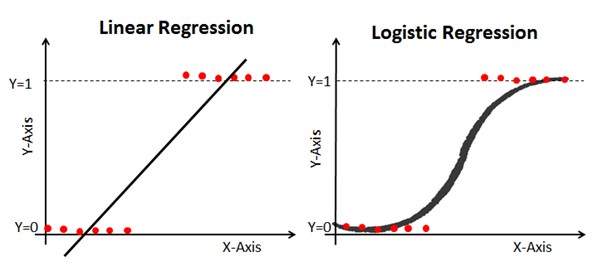
Linear versus Logistic Regression
Simple logistic regression analysis is used with one binary outcome and one independent variable. Multiple logistic regression analysis is used when there is a single binary outcome and more than one independent variable.
The outcome in a binary logistic regression is often coded as 0 or 1, where 1 represents the desired outcome. Zero (0) indicates the desired outcome is not present. If you define p as the probability the desired outcome is present, the multiple logistic regression model can be written as follows:
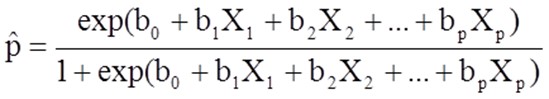
P hat is the expected probability that the outcome is present. The X1 through Xp are the independent variables, and bo through bp are the regression coefficients. The intercept bo and the coefficients b1 through bp are calculated for the relevant data, and the probability for that combination is calculated as above.
The MBB helped the team input the data into a statistical software package, which would do all the calculations and provide the final prediction formula so the probabilities of winning the bid could be determined. The Xs were the factors mentioned above: interest rate, term length, risk, desired rate of return, points, estimated rate of inflation, size of loan, and credit worthiness of the client.
The challenge was getting people to understand the method and trust the outcome
Since all the calculations were done by the computer, there was no real concern about understanding the underlying calculations. The big challenge was having the team understand the concept of predicting a probability rather than a numerical value as they were accustomed to when using multiple linear regression.
To try and convince the team of the power of multiple logistic regression with a binary outcome, the MBB did a series of computer runs using the past 20 bids. In each case, he input the factors and computed the probability of getting the loan. He then compared that with the actual outcomes of the bid. The team was impressed that, where the probability of success was predicted at 75% and above, the company had won the bid.
The win ratio and probability of loan bids increased by 9.8%
Once bids are opened, they are now available to the public. The company collected information about the factors used by their competitors for loans the company lost. They used the information to do simulated runs using logistic regression. In almost all cases, the predicted probability of winning was high for their competitors. Inserting the factors they used on those same bids resulted in lower probabilities than those of their competitors.
The team used the binary multiple logistic regression model for the next five bids. They adjusted the levels of the different factors and used the prior competitive information until they had a bid with a 75% or higher probability of winning. That is what they submitted.
To everyone’s surprise, except the MBB, they won 4 of the 5 bids. The company then made it standard practice to evaluate and submit bids using binary logistic regression.
3 best practices when implementing binary logistic regression
While it might seem scary to use this tool for such a high-impact decision, have faith in the technique, and follow the tips below.
1. Identify the relevant factors
The outcome of any regression is dependent on the factors you select as your independent variables. Be sure they make sense and are relevant.
2. Decide on what your outcome probability represents
Are you trying to predict the probability of success or failure? Be sure you properly enter the correct value, either 0 or 1, in the dialog boxes of your statistical software.
3. Have a success probability in mind
What probability of success will you be satisfied with? Adjust your factor settings until you achieve that number, keeping in mind the validity of your selected factor values.
The use of binary logistic regression was a success
Binary logistic regression is like other regression techniques except for the fact that the predicted outcome is not a numerical value but a probability of either success or failure as you define it. Adjust and refine your factor settings until you achieve a probability that’s acceptable to you.
While binary is the most common application, there are two other forms of logistic regression. Here is a description of all three:
- Binary logistic regression: The response variable can only belong to one of two categories: pass or fail
- Multinomial logistic regression: The response variable can belong to one of three or more unordered categories: sweet, sour, salty
- Ordinal logistic regression: The response variable can belong to one of three ordered categories: high, medium, or low