
If you have two sample groups of continuous data and want to determine whether their means came from the same population, you would use a 2-sample t test. But, what if you had more than two sample groups? Using ANOVA is a very efficient way to test the three or more group means and whether they came from the same or different populations.
Overview: What is ANOVA?
ANOVA was developed in 1918 by the famed statistician Sir Ronald Fisher. Previously, it was suggested you use a 2-sample t test for two groups. But what if we had 3 or more groups? For 3 samples, A, B and C, you could compare A to B, A to C and B to C, using a series of 2-sample t tests and an alpha risk of 0.05 for each comparison.
With this approach you have a greater than 0.05 chance of being wrong. The greater the number of group samples, the greater the number of comparisons and the greater the chance of being wrong.
Overall alpha = 1 – (1-alpha per comparison)number of comparisons
With three groups and an alpha of .05 the resulting alpha would be
Overall alpha = 1 – (1 – .05)3 = .143
You can see that your original alpha risk of 0.05 has increased to 0.143. What if there was a test in which there was only one comparison, but it was designed so it could handle 3 (or more) samples?
ANOVA is based on the F ratio which allows you to compare the denominator to the numerator as a single comparison. The denominator is calculated to establish the amount of variation you would normally expect. It becomes a sort of standard of variability against which you check all others. The numerator is the others that are being checked. It is also referred to as the Signal/Noise ratio. You are looking for a Signal that the group means are different. Noise will mask the ability to do that.
When the F ratio value is small (close to 1), the value of the numerator is close to the value of the denominator and we cannot reject the null hypothesis that there is no difference between the population means from which the data came from.
However, when the F ratio is sufficiently large, that is an indication that the value of the numerator is substantially different from the denominator and we reject the null. But where do the actual values for the denominator and numerator come from?
The denominator value comes from the within group variability, while the numerator value comes from the between group variability. Both values are calculated using a sum of squares approach. Assume you have four groups. Here is how you would graphically represent how you compute the sum of squares values.
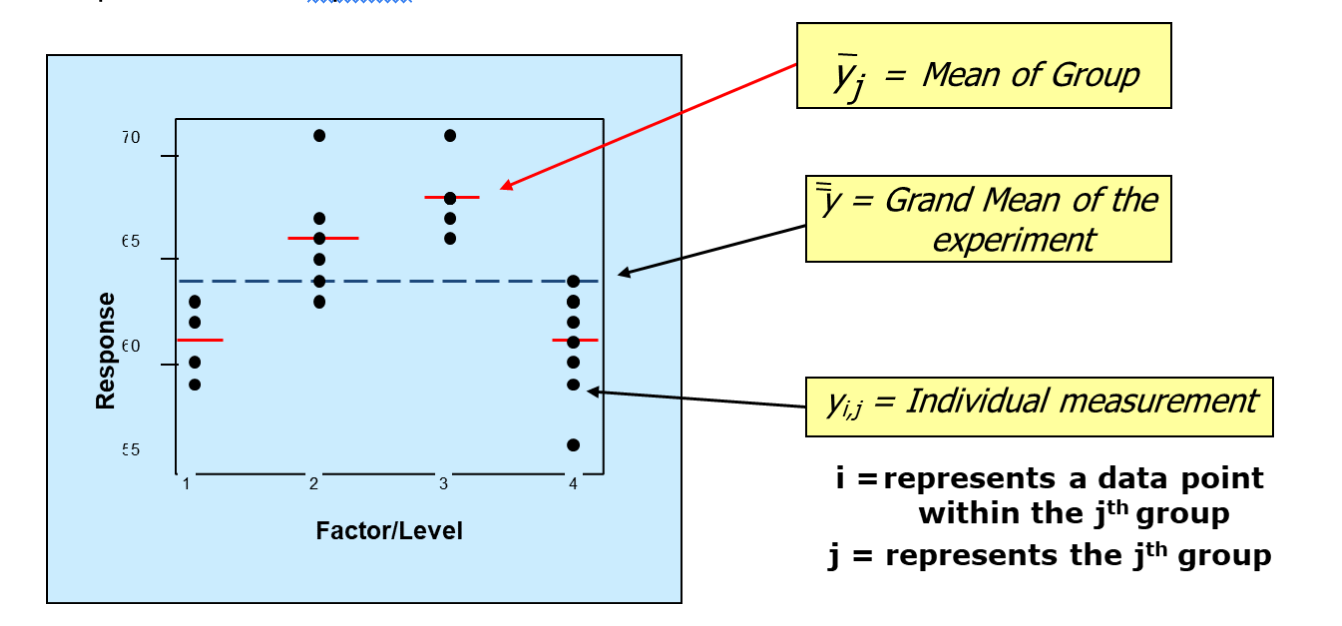
Now for the actual formula and calculations:
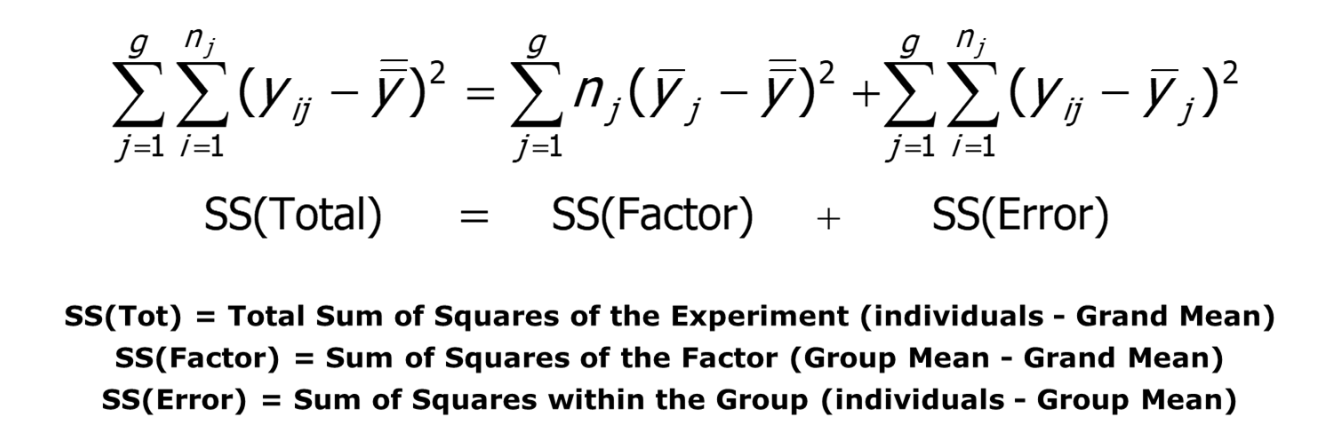
There are a number of underlying assumptions about ANOVA which you must confirm. Here are the primary assumptions:
- Model errors or residuals are assumed to be normally distributed with a mean of zero and randomly distributed
- The variance is assumed constant for all groups
- The samples are assumed to come from normally distributed populations
3 benefits of ANOVA
ANOVA is powerful and efficient with the following benefits:
1. Requires less computations
The computations for an ANOVA of three or more groups is considerably less than if you attempt to do multiple t test comparisons.
2. Uses the concept of variation to test means
By using within and between variation for your groups you are able to transform the variation information into a comparison of means.
3. Can be used for any number of groups
ANOVA can be used for comparing the means of three or more groups versus just two groups for a 2-sample t test.
Why is ANOVA important to understand?
There are a number of concepts in ANOVA you will want to understand to use it properly.
Signal/Noise ratio
Even though you are testing for differences in means, ANOVA uses a ratio of variation (within and between) to draw conclusions about the difference in group means.
Limitations of the assumptions
As in all statistical tools, you must comply with the underlying assumptions of the tool to have confidence in your results and conclusions. Normality and equal variances of each group are important assumptions to be met.
Can be used for one or two response variables
There are two versions of ANOVA. One is called One-way and the other is called Two-way. One-way consists of a single continuous response variable while the Two-way ANOVA can be used when you have two continuous response variables.
An industry example of ANOVA
A Product Manager was trying to develop a better process for signing up customers for equipment placement in retail stores. Most of his issues revolved around getting customers approved for new equipment. The Master Black Belt ,assigned to his division, suggested he use ANOVA to investigate whether there were any statistically significant differences between his three distribution channels.
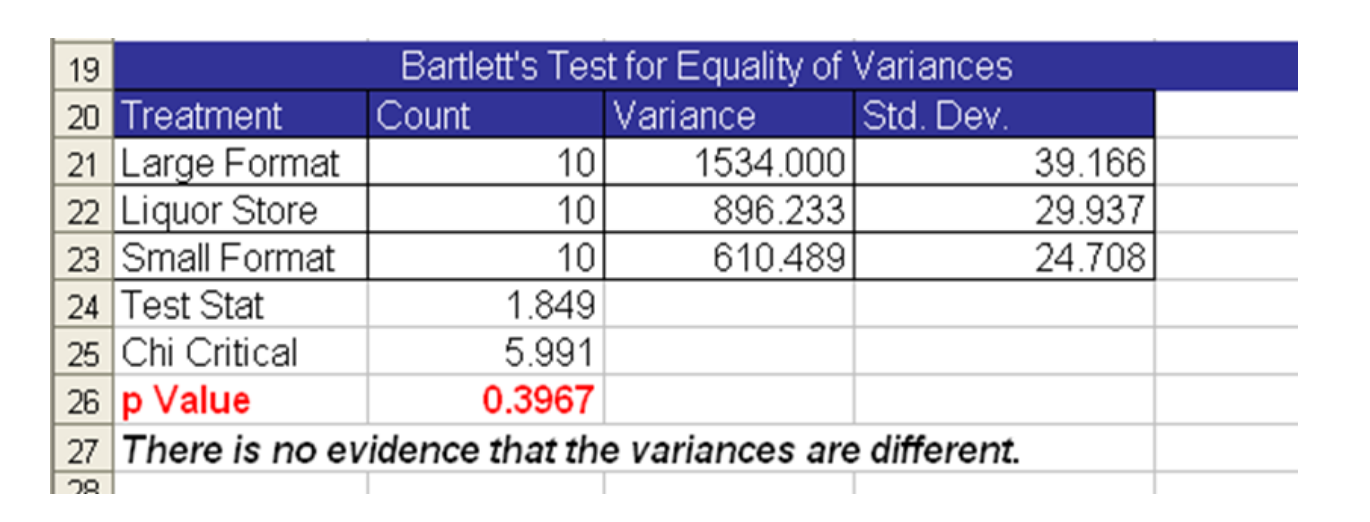
His first task was to confirm his data met the assumptions of normality and equal variance. Below is his computer output. Note the p-values are higher than 0.05 indicating the data in his three groups are not different than normal. Likewise the three groups had approximately the same variances.
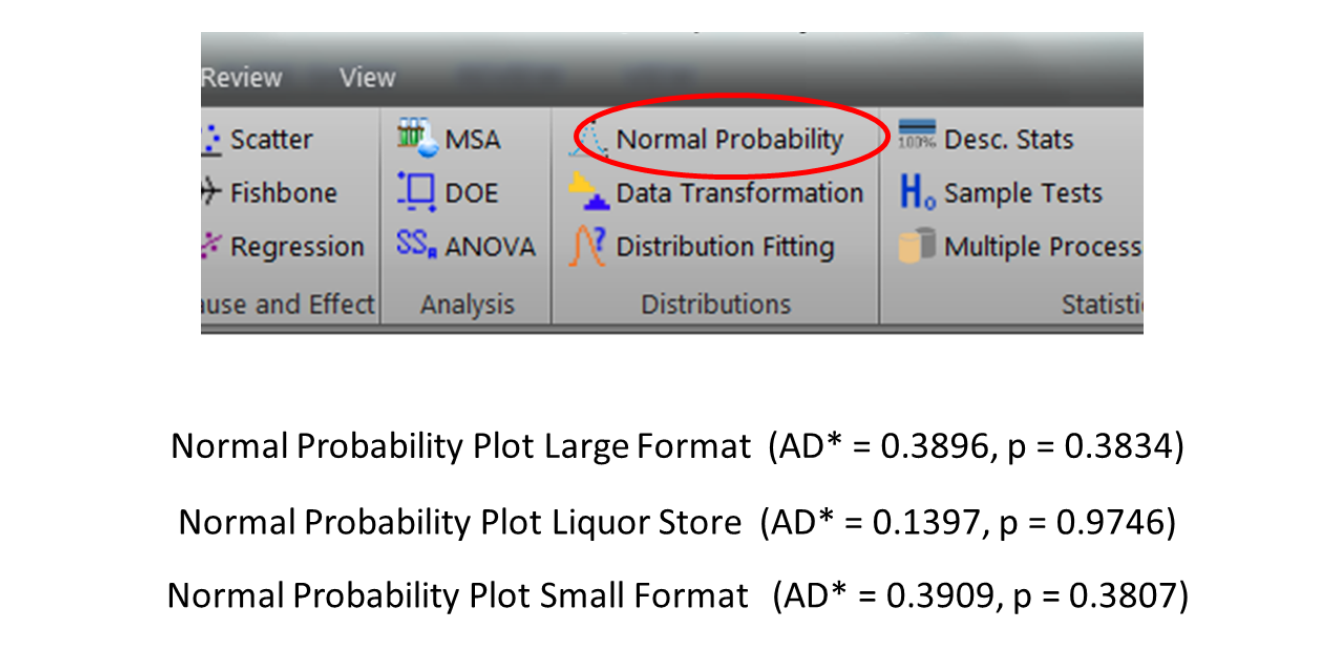
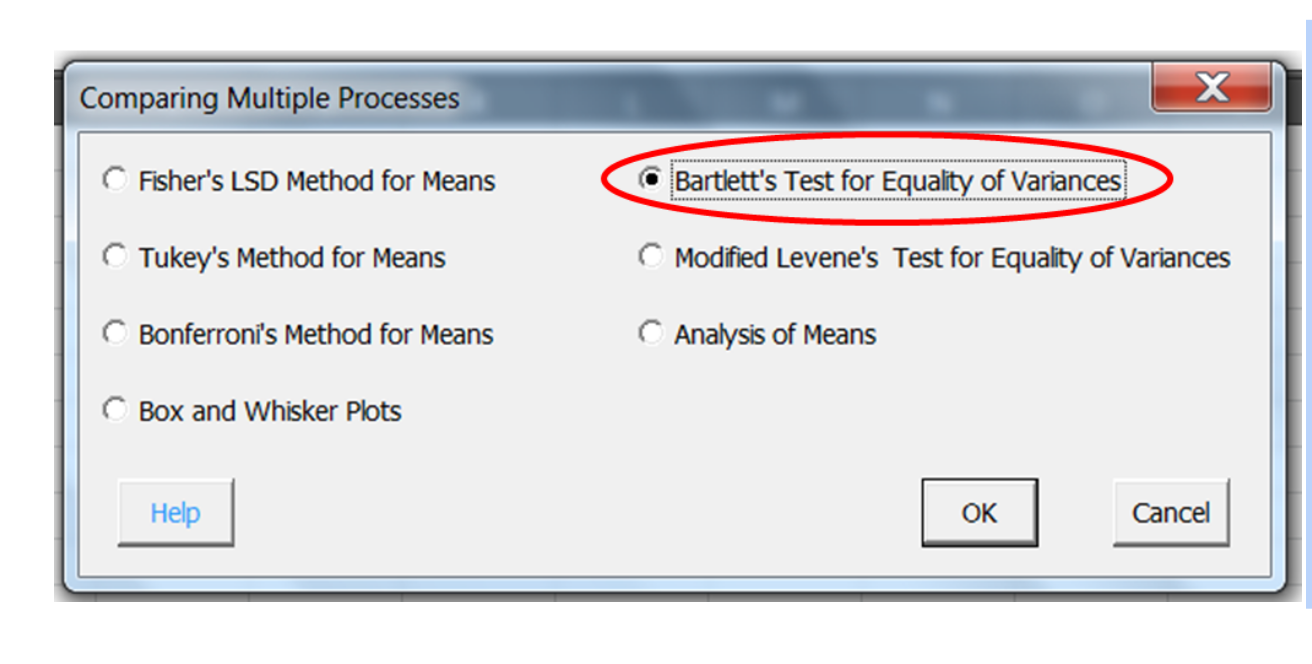
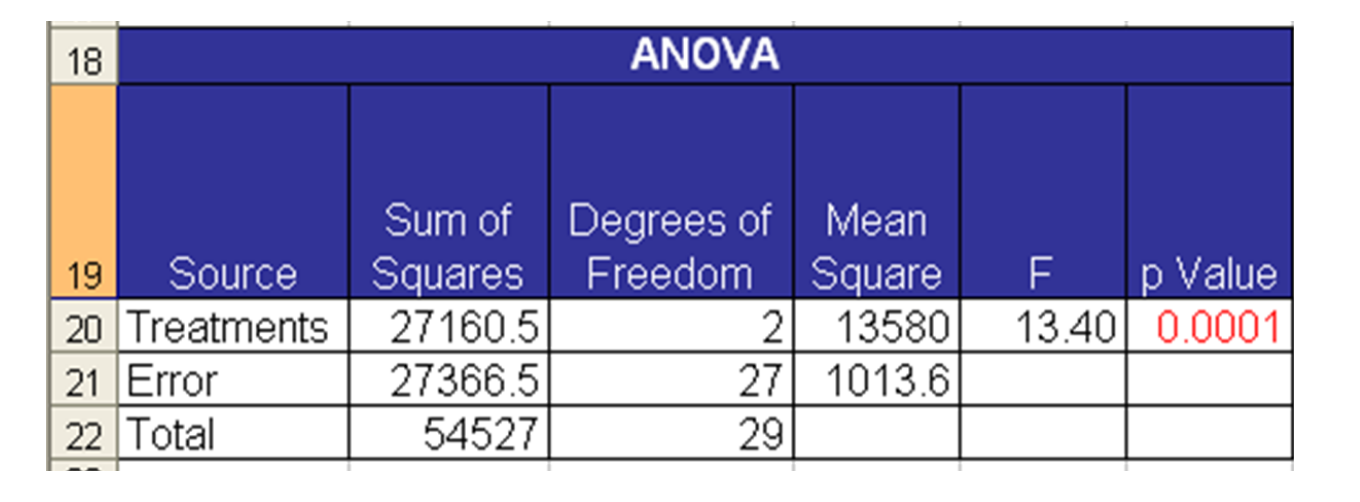
The ANOVA table, based on the low p-value indicates there is a difference between the three groups.
The Product Manager identified which group had the fastest signup times, found out what they were doing and shared the best practices with the other groups. After one month, all three groups were signing up customers faster than before.
3 best practices when thinking about ANOVA
Here are a few hints to help you efficiently utilize ANOVA.
1. Do an MSA
It is recommended that you do a Measurement System Analysis (MSA) on your measurement system to have confidence that the data you are analyzing is accurate and valid.
2. Confirm assumptions
You will need to confirm that you have met the assumptions for using ANOVA otherwise your results and conclusions may be incorrect.
3. Select a reasonable alpha risk
Your selection of an appropriate alpha risk will impact the power of your ANOVA. Power is the ability to see a difference in your groups if one exists. You will want to maximize your power. As alpha goes up so does the power of your test.
Frequently Asked Questions (FAQ) about ANOVA
What’s the difference between ANOVA and t-test?
The t test can be used for one or two sample groups. ANOVA should be used for three or more groups of data.
Can I use ANOVA if the variances of my data groups are not the same?
No. Equal variance is one of the underlying assumptions for using ANOVA. Unequal variances or outliers in the data will negatively affect the outcomes of the statistical analysis.
What are some of the assumptions for using ANOVA?
ANOVA assumes that the data for each group is normally distributed. ANOVA also assumes the variance among the groups should be approximately equal. Finally, ANOVA also assumes the observations are independent of each other.
Wrapping up ANOVA
ANOVA is a powerful statistical method using within and between variation of three or more groups to determine whether there is a statistically significant difference between the means of the populations from which the three or more groups came from.
Recapping the ANOVA methodology:
- Select a sound sample size and factor levels
- Randomly conduct your trials and collect the data, watch for outliers
- Conduct your ANOVA analysis
- Follow up with Pairwise comparisons if needed (i.e., Tukey)
- Examine the residuals, variance and normality assumptions
- Generate main effects plots, interval plots, etc.
- Draw conclusions