
Several statistical tests have underlying assumptions of a specific type of distribution which is required for the test results to be valid. But what if your data distribution does not meet that assumption? A non-parametric test might help.
There are several hypothesis tests which assume your data has a specific distribution. For example, a 2-sample t-test has an underlying assumption that your data follows a normal distribution. Tests with assumptions of a specific distribution are called parametric tests. Tests that do not require a specific distribution to be valid are called non-parametric tests.
Overview: What is a non-parametric test?
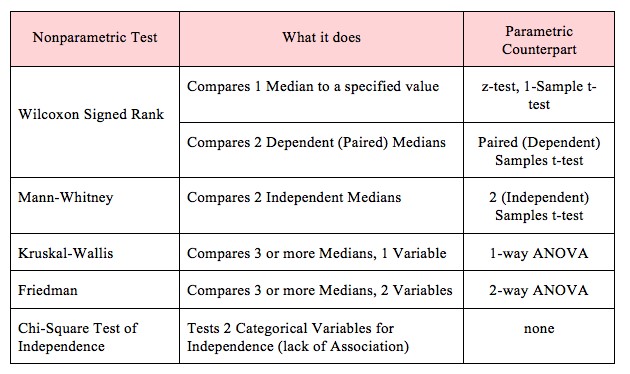
Those parametric tests assuming a normal distribution make use of the mean or average of your data set to draw conclusions about your data. The equivalent non-parametric test uses the median of the data rather than the mean. The table below shows common non-parametric tests, what they are used for, and their equivalent parametric test:
An industry example of a non-parametric test
William, the company Six Sigma Black Belt (BB), was asked to analyze whether the retrofit of a key piece of equipment helped increase the speed of the machine. Since William was comparing a before and after condition and the data was continuous in nature, he chose to use a 2-sample t-test.
Unfortunately, when he analyzed whether the data was normally distributed, he found the data was not normal since time data is generally skewed. Since his sample size was only 12 readings, he decided to use the non-parametric Mann-Whitney hypothesis test. Upon analyzing the output of the test, he concluded there was a statistically significant increase in machine speed.
Frequently Asked Questions (FAQ) about a non-parametric test
What is the difference between a parametric and non-parametric hypothesis test?
A parametric test has an assumption that your data follows a specific distribution. A non-parametric test does not have a distribution assumption.
A parametric test usually uses the mean of the data so what does a non-parametric test use?
An equivalent non-parametric test uses the median of the data.
Which test is better – parametric or non-parametric?
The parametric test will have more power. Power is defined as the probability of finding a significant effect if one exists.
Can I use a parametric test even if my data is non-normal?
A parametric test will work with non-normal data if certain sample size considerations are met. The table below shows some of those sample size considerations:
