Key Points

• Random variation is a deviation from a standard distribution independent of inputs or biases.
• Randomness directly correlates with the precision of your processes.
• Learning how to account for and overcome randomness can lead to better deliverables.

If you’re interested in the statistical concepts surrounding random variation, we will provide the statistical definition and explore how it might apply to your organization. 

For those more interested in what it means in practical terms, we will explore the definition and application in terms of its benefits and how it can be used to better manage your organization.

Overview: What Is Random Variation?

One of the best definitions for random variation appears in the dictionary of the iSixSigma.com website: 

The tendency for the estimated magnitude of a parameter (e.g., based upon the average of a sample of observations of a treatment effect) to deviate randomly from the true magnitude of that parameter. Random variation is independent of the effects of systematic biases. In general, the larger the sample size is, the lower the random variation is of the estimate of a parameter. As random variation decreases, precision increases.

In other words, everything varies, whether it be the dimensions of your product, your weight, your manufacturing processing time, the time to get to work, or your blood pressure. Over time, you would expect the variation of those measurements to form some kind of statistical distribution that would approximate the underlying population of whatever you are measuring. 

That underlying distribution will have a calculated central tendency, variation, and shape. At any point in time, the measurement you take will vary and can come from any place in that distribution.

If there is random variation, you will not be able to predict the exact value of the next measurement. You might be able to calculate the probability of what the next value might be — or even calculate a range of values within the next measurement that might fall. We can call that a confidence interval.

How Random Variation Affects Your Processes

While the statistical properties are interesting, what might be more important for you is how the concept of random variation impacts your ability to manage your process. If your process is exhibiting random variation, or what Dr. W. Edwards Deming called common cause variation, then your process is predictable and in what might be called a steady state. Deming distinguished common causes from special causes. Special cause variation is unpredictable and a function of some unexpected intervention in your process.

For example, the fill level of your bottle will have some variation as a function of the variation in your fill equipment, liquid, temperature, and run speed. That is the steady state given the combined effects of the variation in your process elements. It is expected and, over time, will form some distribution. 

However, if one of your fill nozzles starts to clog up, there will be a variation in fill that is a function of a specific and assignable cause. That would not be expected or predicted until after its occurrence. That would be non-random variation — or special cause variation.

You can use a control chart to distinguish between a random (common cause, predictable, noise) variation and a non-random (special cause, unpredictable, signal) variation.

Chaos and Order

Try as you’d like, there is no way of truly eliminating randomness from your processes. Things can and will go wrong. As such, learning how to account for random variation and overcome it can be the fast track to success when it comes to making your processes the best they can be.

Benefits of Paying Attention to Your Variation

Knowing whether your process is exhibiting random or non-random variation will help you properly respond to the signal you receive from your control chart.

1. Proper Response

If your process is exhibiting random variation then any improvement will require a fundamental change in the process. If the process is exhibiting non-random variation, then you will need to identify the reason for that assignable cause and then take action to either eliminate or incorporate changes to maintain an improved state or eliminate a negative impact. 

2. Predict

If you are taking sample measurements and the process is demonstrating random variation, you’ll be able to do some level of prediction of future values.  

3. Assess Changes

If your process is demonstrating random variation and you make a change, you will have confidence that, if you see an impact due to your change, it will be real and believable.

Why Is Random Variation Important to Understand?

The concept of random variation, or noise, is central in statistics. You will want to understand what random variation is and its implications for taking the appropriate actions in your process.

Underlying Assumption

Most statistical tests will have an underlying assumption that the data you’re analyzing was created by a random process. If not, your results may be inaccurate because of the influence of non-random variation.

Desired State

You should strive to achieve random variation in your processes. Random variation does not imply that everything is OK or good, but merely that the process is predictable and steady state. From there, you will want to evaluate whether that steady state is satisfactory or needs to be improved.

For example, why do you think your doctor wants you to fast before a blood test? Is it to be mean (especially if your appointment is in the afternoon)?

No, your doctor wants you to only exhibit random variation in your body processes and not have the influence of special cause variation, so your test results can be considered representative of your true steady state. That doesn’t mean elevated blood pressure is good, but at least your doctor knows that it exists. From there, he or she can have the proper response. 

Improper Response

Unless you have a good understanding of random variation, you may inadvertently believe you have non-random variation when you don’t. This would cause you to try and find an assignable cause when none exists, or make changes as a result of an individual observation that would be tantamount to tampering with the process.

An Industry Example

Unfortunately, many managers don’t understand or appreciate the concept of random variation. For example, a manager in the finance department of a B2B online business was getting complaints from the CFO that invoices were slowly getting out to the customer, and thus cash flow was being negatively impacted.

The LSS Master Black Belt (MBB) investigated and found out that, as a result of their LSS training, the manager was in control of charting the invoice processing time. That was a good thing. When the MBB started questioning the manager about how he uses the control chart, he realized what the problem was. The control chart had all of the points within the upper and lower control limits so the process was demonstrating random variation.

The manager was reacting to high and low points without appreciating whether the process was exhibiting common or special cause variation. It turned out that when the manager saw a “high” point on the control chart he initiated a search for the root cause. And when he was happy with a “low” point, he didn’t do anything except say “Great job!” 

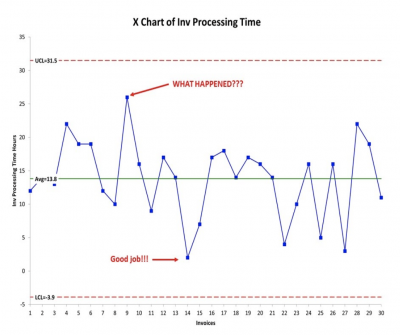
The manager should have realized that the process was stable and showing random variation so the appropriate response should have been to change the process to reduce the overall variation — and if desired, to lower the average processing time.

Random Variation Best Practices

To manage your process by properly using the concept of random variation, you should consider the following best practices.

1. Collect Your Data in a Random Manner

To get a picture of the true random variation of your process, you should randomly collect your data. Introducing any bias in your data collection will impact the randomness of your variation.

2. Use the Appropriate Statistical Tools to Determine If You Have Random Variation

As has been explained before, the statistical control chart is the best tool for determining whether your process is generating data in a random pattern or not. 

3. Provide a Proper Response

You should react to random variation by seeking to improve your process if it’s not capable of meeting your specs, targets, or expectations. If you have non-random variation, you will need to investigate why and then take the appropriate steps to either incorporate or eliminate the reasons why. 

Other Useful Tools and Concepts

Looking for some extra tools? You might do well to learn all about Little’s Law. This basic calculation allows you to readily see how long an order will take before reaching your customers. It has roots in other methodologies but is readily applied to Six Sigma.

Additionally, learning about the application of lower control limits in your control charts can readily let you see the outliers that aren’t making the grade. This works in conjunction with upper control limits and is extremely useful for pinpointing issues in your production.

Conclusion

Random variation is the desired state for your process. It is predictable and consistent. But, it does not mean your process is operating at its best, only that it is steady state. 

The control chart is the best tool for distinguishing between random variation and non-random variation. If you want to improve your process, then make sure you are only seeing random variation. If you have non-random variation, find out why, and deal with the root cause(s). Hopefully, then you’ll have a process showing only random variation.

The image featured at the top of this post is ©Tint Media/Shutterstock.com.