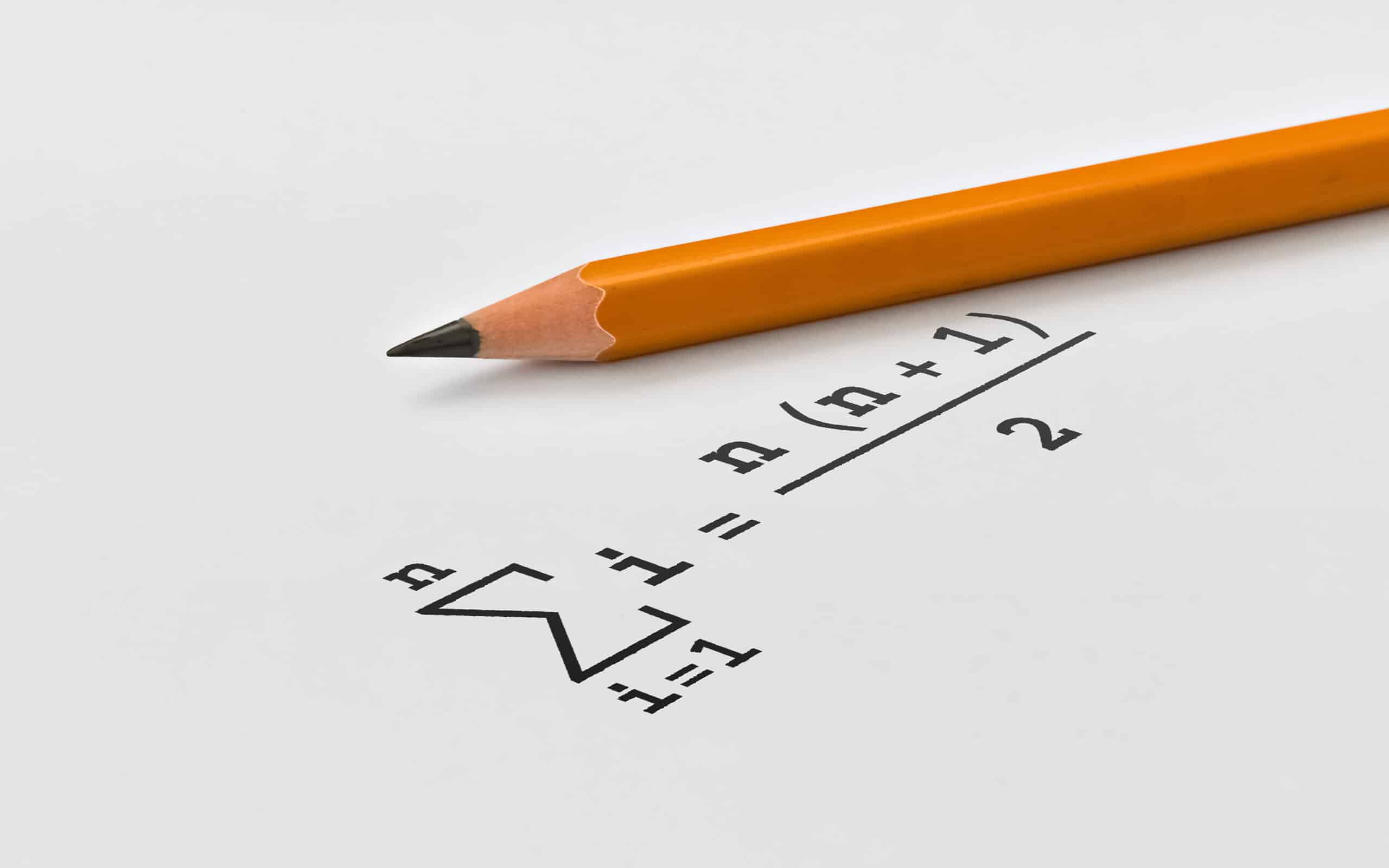
The meaning of sigma in statistics is a function of whether you use the upper or lower case of the letter. The uppercase use of sigma denotes a summation while the lowercase represents a measure of variation.
Overview: What is sigma?
Below are the uppercase and lowercase symbols for sigma:
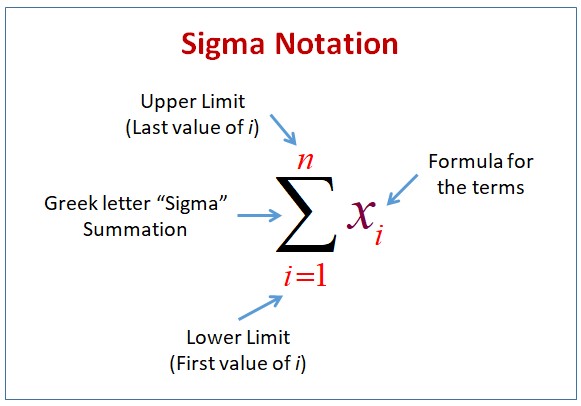
When used in the uppercase, it indicates a summation of values as shown below:
A lowercase sigma signifies and represents the population standard deviation of a set of quantitative data. Interestingly, the formula for the standard deviation includes the uppercase notation of sigma. See the formula below:
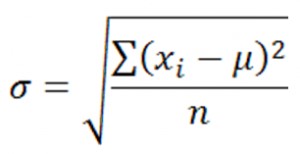
Lowercase sigma is also referred to in the context of Six Sigma. In this case, it is a measure of process capability The term Six Sigma means that the closest specification of a process or product is six standard deviations away from the mean of a normally distributed set of data. This capability is defined as having only 3.4 defects per one million opportunities often referred to as 3.4 parts per million (ppm).
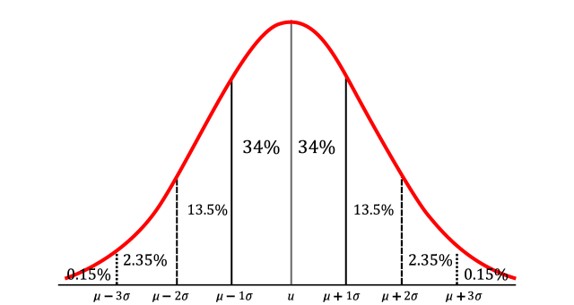
Another use of lowercase sigma is in the Empirical Rule, which describes the distribution of data in a normal distribution. When adding and subtracting various numbers of standard deviations from the mean, you will encompass different percentages of the total data set. Below is a graphic of the Empirical Rule.
An industry example of sigma
Here are a few examples of how sigma can be used in statistical calculations.
![]()
If I wanted to add up the numbers above, I would use the following format of sigma: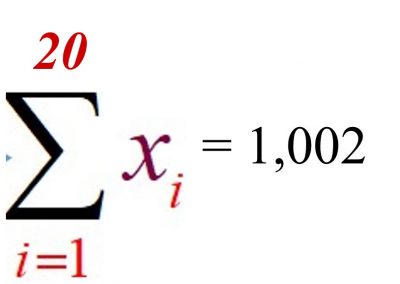
Assuming the data set was the population data, I would use the following format of sigma for calculating the population standard deviation:
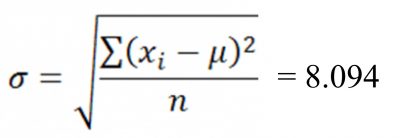
Frequently Asked Questions (FAQ) about sigma
What is the symbol used for the sample standard deviation?
Lowercase sigma is used for the population standard deviation while the letter s is used for the sample standard deviation.
What is the difference between lowercase sigma and lowercase sigma squared?
Lowercase sigma is the notation for the population standard deviation. Lowercase sigma squared is the notation for the population variance. In other words, lowercase standard deviation is the square root of the population variance.
What is sigma a measure of?
Sigma or standard deviation is a measure of the variation in a set of data. Simply stated, it is the average distance that each point is away from the mean of that data set.