
The analysis of variance (ANOVA) procedure is conducted during the Analyze phase of a Six Sigma project. Assessing results from an ANOVA table can present a challenge making it difficult to understand precisely what conclusions to draw. However, there is an easy way for Master Black Belts to explain to their charges the ANOVA procedure.
During Six Sigma training, the practice of assessing relevant p-values is encouraged, though typically without comment as to how the computations are performed. This can lead to some misconceptions unless there is some familiarity with the mechanics behind this mathematical procedure.
The ANOVA Table
The derivation of the ANOVA procedure is widely credited to R.A. Fisher and popularized through his 1925 landmark book, Statistical Methods for Research Workers. The table currently used when obtaining output from the ANOVA procedure is remarkably similar to Fisher’s original construction, which consisted of the following four columns:
- Sources of variation
- Degrees of freedom
- Sums of squares
- Mean squares
The addition of the F-statistic into a fifth column and the corresponding p-values into a sixth column is now common practice. The following example illustrates the use of an ANOVA table.
An experiment was conducted to assess the effect on yield in a chemical reaction at four temperatures (100°C, 120°C, 140°C and 160°C). Results from the experiment using a one-way ANOVA are shown in Table 1.
| Table 1: One-Way ANOVA: Yield Versus Temperature (C) | |||||
| Sources of Variance |
Degrees of Freedom |
Sums of Squares |
Mean Squares |
F-Statistic | P-Value |
|
Temperature (C) |
3 |
457.3 |
152.4 |
5.68 |
0.003 |
| Error |
36 |
966.6 |
26.9 |
||
| Total |
39 |
1423.9 |
|||
The Analysis of Total Variance
The first challenge when teaching ANOVA is why this procedure is called the analysis of variance when it typically assesses a comparison of the treatment means. To understand why the title, ANOVA, makes sense, it is useful to consider the final row of information in the table: “Total … 39 … 1423.9.” The value of 1,423.9 is referred to as the total sum of squares and is merely the numerator in the familiar formula for the sample variance:
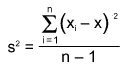
There are 40 resulting values from the experiment and the corresponding degrees of freedom in the ANOVA table is 39, one less than the total number of observations. When the sum of squares is divided by the degrees of freedom, it yields the sample variance. The ANOVA procedure seeks to decompose the total sample variance into the corresponding sources of variation. The example addresses the amount of variation between the treatments (the four temperatures) with respect to the variation within the treatments (denoting the error). Fisher’s original description of the ANOVA methodology is insightful:
“When the variation of any quantity (variate) is produced by the action of two or more independent causes, it is known that the variance produced by all the causes simultaneously in operation is the sum of the values of the variance produced by each cause separately…The property of the variance, by which each independent cause makes its own contribution to the total, enables us to analyze the total, and to assign, with more or less accuracy, the several portions to their appropriate causes, or groups of causes.”
Sources of Variation
If a relatively large portion of variation is explained by the temperature effect, there is evidence to suggest that temperature has an effect on the response variable of yield. The sums of squares for the temperature effect is 457.3. Therefore, roughly a third of the total variation is explained by this effect. Note that this fraction (457.3/1423.9 = 32%) is the most widely used R2 value.
It is imperative to consider not only the individual sums of squares, but also the amount of information used to obtain the degrees of freedom. The sums of squares for the temperature effect and the residual error are weighted by the degrees of freedom to obtain a valid comparison. The comparison is illustrated in the column of results in the mean square column (column 4 in Table 1) where the sums of squares are divided by the appropriate degrees of freedom.
A large ratio of the mean squares (the F-statistic) implies that the amount of variation explained by temperature is large in comparison with the residual error. For this example the F-statistic is 5.68, with an associated p-value of 0.003. Since the p-value is less than 0.05, the temperature effect is statistically significant at thea= 0.05 level (0.003 < 0.05). Therefore, the temperature effect is an important factor for consideration.
An Analogy for Sums of Squares and Degrees of Freedom
The following analogy may help when presenting the idea of sums of squares and degrees of freedom to those not familiar with the concept behind ANOVA.
Consider the popular arcade game, Pac-Man. Regard the total sum of squares as the total number of pellets that Pac-Man must eat, and the total degrees of freedom as the amount of lives available. Using the data from the chemical reaction example, approximately 457 (about one-third) of the pellets were consumed with only three of the available 39 lives used. This analogy is especially helpful when considering multiple sources of variation as with a two-way random effects model in a gage repeatability and reproducibility (Gage R&R) study, as well as within other designed experiments. (Burdick, R. K., Borror, C. M. and Montgomery, D. C. [2003], “A Review of Methods for Measurement Systems Capability Analysis,” Journal of Quality Technology, Vol. 35, No. 4)