One of the most popular metrics used in assessing Six Sigma projects, both DMAIC (Define, Measure, Analyze, Improve, Control) and Design for Six Sigma (DFSS), is defects per million opportunities (DPMO). This measurement is the average number of defects per unit observed during an average production run divided by the number of opportunities for making a defect on the product. Then the number is normalized to one million. A defect is defined as a failure to conform to requirements. Those requirements are articulated in the specification or tolerance of the products or processes.

Tolerances should be determined in product or process development. They should be established in order that the products or processes may be assembled easily, and so that they can perform their required function with minimum adjustment. Properly designed specifications can reduce the DPMO. A too-tight tolerance specification can ensure functional requirements, but it is not cost effective. A too-loose tolerance specification will bring low assembly process, but frequent rework would likely be required to maintain performance.

Two different methods can be used to determine tolerance specifications. One is a conventional method that depends upon designers’ experiences and perception. The other one is a loss function method that is based on cost of poor quality. The loss function method also is called method of tolerance optimization. Here is how these two methods work on a simple gasket placement issue.

Problem Statement

Certain electronic components on a wireless communication PCB need to be shielded, and the shield gasket must sit on the gold trace around the components such that it does not touch or impinge the components. Touching electronic components may disturb the function of the system constructed by those components. How well the components are shielded depends on:

• The variability of gasket placement to the shield
• Closest distance between components and the gold trace
• PCB and the shield displacement

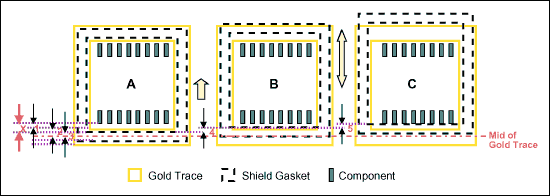
In the figure, A is the intended design: the shield gasket perfectly sits on the middle of the gold trace without touching the base band components. B is the situation where the displacement between shield and PCB happens. C is the situation where B happens plus the variability of the shield gasket placement. In this example bias is not considered. Nomenclatures on the model are:

• X_C-GT is the distance between base band components and the gold trace.
• X_H-GT is the half width of the gold trace.
• X_H-SG is the half width of the shield gasket.
• D_PCB-S is the deviation due to displacement between PCB and the shield.
• D_SG is the deviation of shield gaskets.

The intended distance between the gasket and the components is the distance between electronic components and the gold trace plus the difference between the half width of the gold trace and the half width of the gasket, that is:

X = X_C-GT + (X_H-GT – X_H-SG )

Deviation of the gasket placement is the displacement between PCB and the shield plus the sum of the variability and the bias of the shield gasket, that is:

Deviation = D_SG + D_PCB-S

The shield gasket will not touch or impinge the base band components if Deviation is less than or equal to X. For simplicity, assume X = 0.5 mm. Thus, Deviation is almost equal to 0.5 mm

Conventional Method

The conventional method for establishing tolerance is to obtain an algebraic sum (linear form).

Deviation = D_SG + D_PCB-S

This equation is a generic form for many known conventional tolerance design methods such as root sum of squares (RSS), worst case, etc. When deviation and deltas are replaced with related variances, this equation can be interpreted as RSS. When deviation and deltas are replaced with Six Sigma tolerances, this equation can be interpreted as Six Sigma worst case. If the distributions of the terms in the equation can be estimated, a Monte Carlo simulation can be run to find the deviation statistics.

Tolerance design is now performed by the following procedure, based on trial and error:

1. A tolerance that is possible and appears under normal production circumstance is allocated to each component. In this example, the chosen gasket placement tolerance (D_SG) = 0.3 mm and, by default, the PCB/Shield stack-up (D_PCB-S) should be = (0.5-0.3) mm = 0.2 mm, which is obtained from the accumulation formula above.
2. If this accumulation satisfies a standard value that produces satisfactory performance, then end.
3. Otherwise, the tolerance allocationshould be reconsidered. For example, due to manufacturing piece-to-piece variation, D_SG is less than 0.3 mm, but D_PCB-S is more than 0.2 mm.
4. The accumulation is recalculated or tolerance allocation to each component is reconsidered.
5. If the accumulation satisfies the value, then end.

The procedure above depends upon how designers include in their design the sources of variation that inhibit the intended dimensions of a component, such as process capability (piece-to-piece variation), degradation over time/cycle, customer usage and duty cycle, external operating environment, and internal operating environment/interaction with neighboring subsystems.

Loss Function Method

After some algebraic derivations using Taguchi Loss Function, the tolerance of each part is given by the following (see, e.g., Tolerance Design: A Handbook for Developing Optimal Specifications by C. M. Creveling, 1997, pages 237-238 and 229-232):

The tolerance of gasket placement is:

The tolerance of PCB/Shield stack-up is:

In the above formulas:

• D_SG is the tolerance of shield gasket placement.
• D_PCB-S is the tolerance of PCB/Shield stack-up movement.
• D_Deviation is the minimum distance between the PCB ground trace and some components.
• L_Deviation is the loss when the minimum distance between the PCB ground trace and some components is smaller than 0.5 mm. This might be a part of thesafety issue.
• L_SG is the loss when the value of gasket placement is outside confidence interval (gasket placement target +/- D_g).
• L_PCB-S is the loss when the value of PCB/Shield stack-up is outside confidence interval (PCB/Shield stack-up target +/- D_PCB-S).
• b_SG and b_PCB-S are rates of change of D_SG and D_PCB-S, respectively, with respect to D_Deviation.

If L_Deviation, L_SG, L _PCB-S, b_SG and b_PCB-S can be obtained, the equations above can be used to determine tolerance D_SG and D_PCB-S. L_Deviation can be considered as cost of poor quality from the safety issue when the shield impinges the components. L_SG can be calculated as cost of poor quality from the rejected gaskets and rework cost. L_PCB-S can be calculated as cost of poor quality from the rework cost. b_SG and b_PCB-S can be obtained from previous data in process/manufacturing or engineering, or considered as equal to 1 if there is no clue.

If there is no historical data to estimate b_SG and b_PCB-S, the closed loop expressions of the D_SG and D_PCB-S influence with respect to D_Deviation can be derived from the first principle of physics or a response surface of experimental designs. Apply Taguchi Tolerance Design (see, e.g., Quality Engineering Using Robust Design by M. S. Phadke,1989, pages 202-205) to estimate the rates of changes. Tolerance Design assumes D_SG and D_PCB-S are the parameters that can be changed and D_Deviation is the response for which its coefficients can be estimated. These coefficients are therates of the changes.

This method is a method of tolerance optimization that is based on cost of poor quality. This method forces the quality professional to have a good understanding of the sources of variation that inhibit the intended dimensions of a component. Therefore, this method also encourages continuous improvement in all steps of product development and production life cycles.

The two methods can be readily generalized for n components.