
If you are monitoring your process data over time, you might want to place greater emphasis on your most recent data and less on your historical data. This will be very important if your process is not stable but is increasing or decreasing in value.
Overview: What is an Exponentially Weighted Moving Average (EWMA)?
The Exponentially Weighted Moving Average (EWMA) is a quantitative technique used as a forecasting model for time series analysis. The concept of using a moving average is designed to give more weight for newer data points and less for older ones. The weights decline exponentially as the data points get older. An exponentially weighted moving average reacts quicker to recent process changes than a simple moving average which applies an equal weight to all data points in a specified time period.
The only decision you must make when using an EWMA is the value of the parameter alpha. Alpha, which ranges from 0 to 1, determines how important the current observation is in the calculation of the EWMA. Alpha represents the degree of weighting decrease and is a constant smoothing factor. A higher alpha discounts older data faster thereby placing greater relevance on your more current data.
Below is the formula for the EWMA’s calculation:
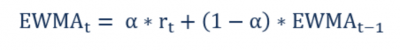
Where:
- Alpha = The weight decided by you
- r = Value of the series in the current period
While EWMA is not used as often in forecasting as other more sophisticated techniques, it is frequently used in control charting of process data. The EWMA chart uses the exponentially weighted moving average of all previous sample means. EWMA weights samples in a geometrically decreasing order so the most recent samples are more heavily weighted while prior samples are given less consideration. The EWMA chart is particularly sensitive to small shifts in the process mean, but does not do as good a job detecting larger shifts as the traditional Shewhart charts (Xbar/R or Xbar/S).
An industry example of EWMA
The company Lean Six Sigma Black Belt was asked to do a control chart for some process data. Since she felt recent process shifts might make current data more relevant, she decided to do a EWMA control chart. For comparison, she also did a standard X/MR chart. Below are her two control charts.
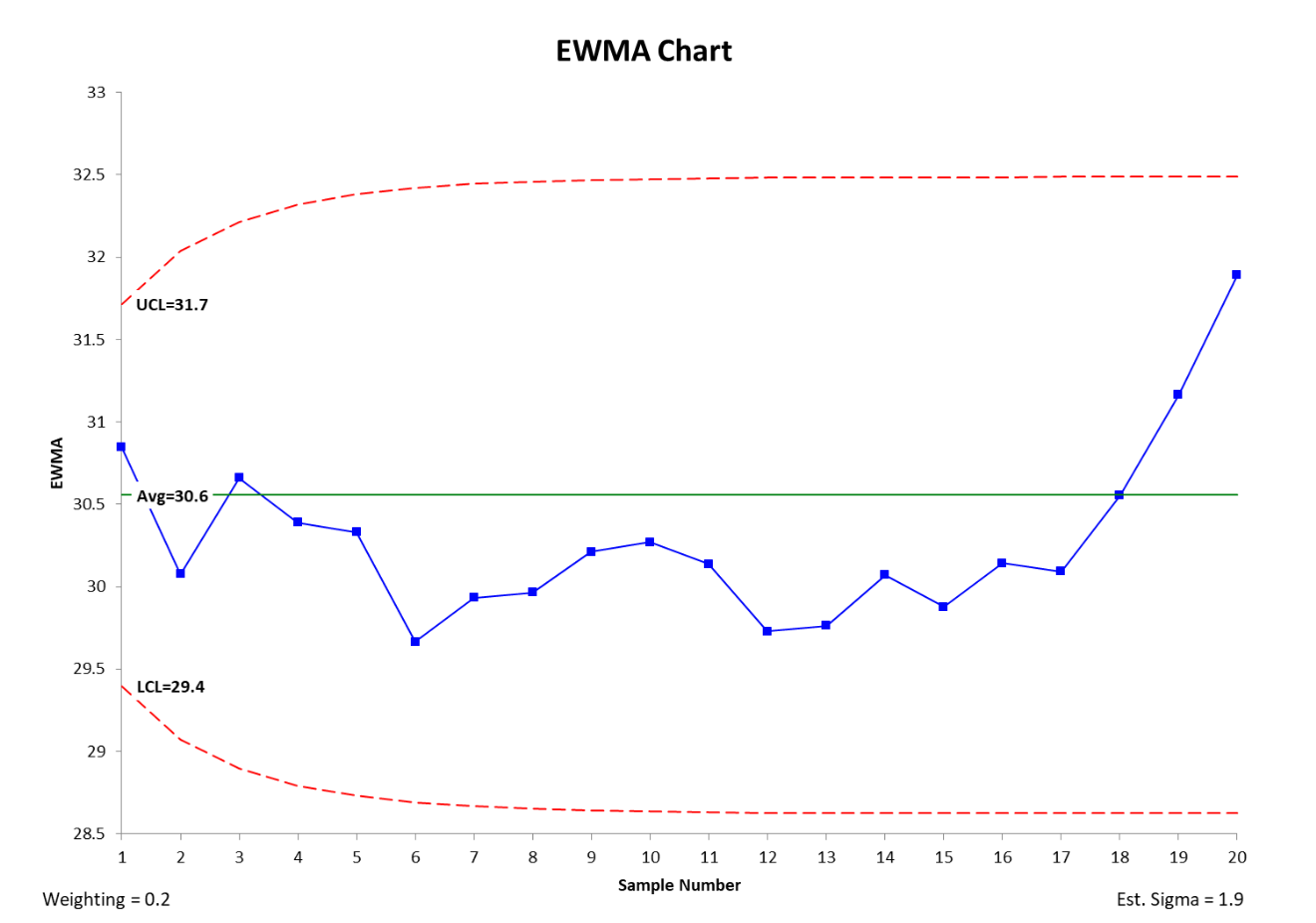
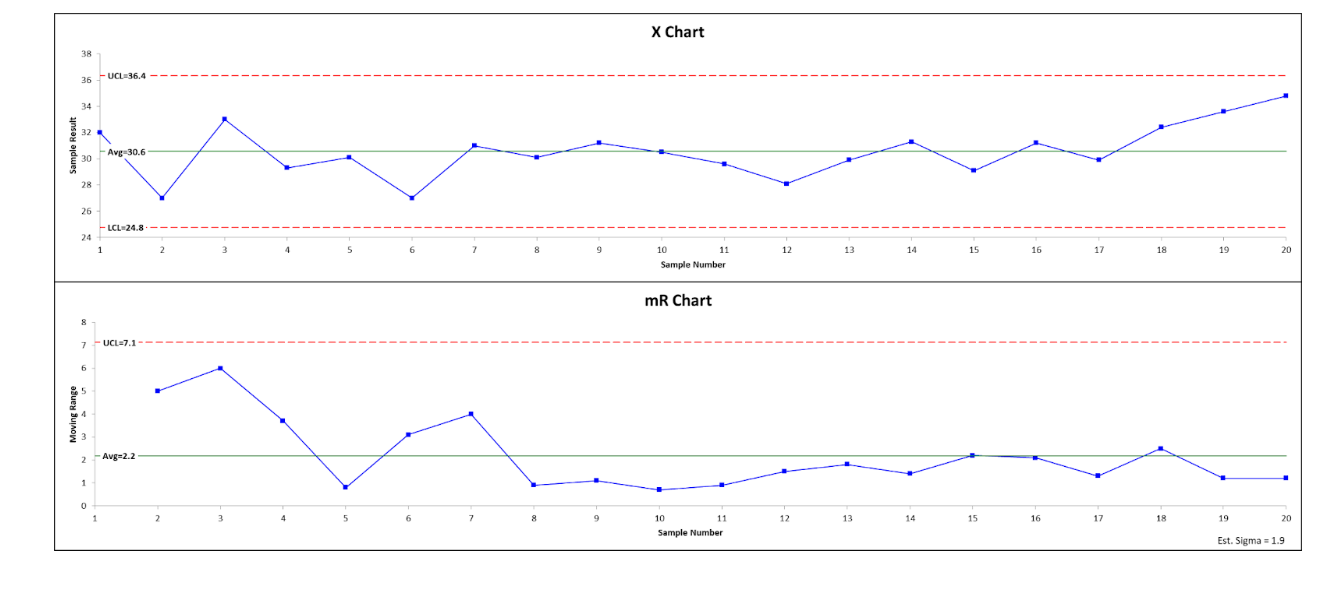
Frequently Asked Questions (FAQ) about EWMA
What is the difference between a simple moving average and an exponentially weighted moving average?
A simple moving average gives equal weight to all data points while the exponentially weighted moving average gives more weight to current data points and increasingly less and less weight to older data points.
What is an advantage of using an exponentially weighted moving average?
The EWMA is more sensitive to changes in the process since it places more emphasis on current data and less on prior data.
What is a major advantage of using EWMA control charts instead of classic Shewhart charts?
The EWMA control chart is more sensitive to small shifts in the process than the traditional Xbar/R or Xbar/S control charts. On the other hand, the EWMA does not capture large shifts as well as the traditional charts.