Definition of Mann-Whitney:
« Back to Glossary IndexWe know we can use the 2-sample t test to see if the means of the two populations where we drew our two sample sets from are the same. But, many times our sample data does not meet some of the assumptions of the 2-sample t test. That’s when we can use Plan B, the Mann-Whitney test.
Overview: What is the Mann-Whitney test?
The Mann-Whitney test is a non-parametric hypothesis test for comparing the medians of two populations when you have two sample data sets. Henry B. Mann and his student Donald Ransom Whitney discussed the development of the test in a 1947 paper.
The 2-sample t test is the equivalent parametric test. Although quite robust, one of the underlying assumptions of the 2-sample t test is that the 2 data sets must be normally distributed. Unfortunately, despite the robustness of the normality assumption, there will be times when you will want to use the Mann-Whitney test to see if there is a difference in the central tendency parameter of the two populations from which your samples came from. In this case, you will be testing medians instead of means as with the 2-sample t test.
The null hypothesis (Ho) for the Mann-Whitney test, also referred to as the Mann-Whitney U test, is that the medians of the two populations are equal. The alternative hypothesis (Ha) is they are not equal. Some assumptions are that you have two independent random samples from two populations having the same shape and whose variances are equal.
An industry example of the Mann-Whitney test
The sales manager was trying to determine whether there was a statistical difference in the sales volume of his two sales offices. He first did a normality test and found the data for sales office 1 was not normally distributed although the data for sales office 2 was. He decided to do a Mann-Whitney test. Below is the output from his Excel based statistical software:
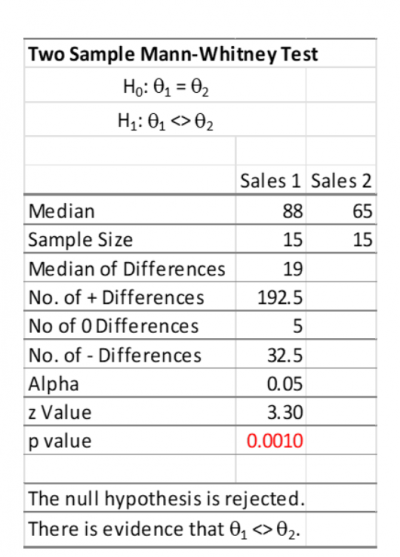
Although it is obvious the medians are not equal (88 vs 65), the p-value of .0010 is very low so the null hypothesis is rejected and the sales manager can conclude sales office 2 median sales are significantly less than sales office 1.
Frequently Asked Questions (FAQ) about the Mann-Whitney test
1. Is the Mann-Whitney Test considered a parametric or non-parametric test?
The Mann-Whitney test is a non-parametric test. It is testing the difference between the medians of two populations and does not have any assumptions regarding the distribution of the data.
2. What is the major difference between the Mann-Whitney test and the 2-sample t test?
The 2-sample t test tests for the difference between two population means and has an assumption the two data sets are normally distributed. The Mann-Whitney test has no assumption about the population distribution and tests for the difference between two population medians.
3. Can the Mann-Whitney test be used for more than 2 sample sets?
No, it is designed for testing only 2 sets of random sample data. You can use the Kruskal-Wallis test or the Mood’s Median test for more than two groups of data.
« Back to Dictionary Index
