
When doing statistical hypothesis testing, it is often assumed that the variances of your sample data groups are essentially equal. Even if you are testing for differences in means, the need to have equal variances will still be an assumption you will need to meet.
Overview: What is homogeneity of variance?
Starting with the premise that you have independent and random groups of continuous data, you may use that data to answer several different statistical questions. If you have two groups of data, you might seek to determine whether the means or variances of those groups are the same or not. In this situation, you will want to use a 2-sample t test. While there is an assumption of normality for the two groups, the t test can be done with an assumption of equal variance or unequal variance (Welch’s t-test).
If you have more than two groups of data and wish to determine whether the means are equal, you will use ANOVA. This test has an assumption of normality for the different groups but also an assumption of homogeneity of variance or, in other words, equal variances.
While there is no normality assumption or homogeneity of variance assumption for your data groups in linear regression, they both are assumed with respect to the analysis of residuals. Here, the residuals should be normally distributed and the variance constant across your range of residual values.
Fortunately, the t-test and ANOVA use the t and F statistics respectively, which are generally robust to violations of the assumption as long as group sizes are equal. If your group sizes are vastly unequal and homogeneity of variance is violated, then the F statistic and test will be biased. When this occurs, the significance level will be under/overestimated, which can cause the null hypothesis to be falsely rejected and you incur a Type 1 error or you lose power in your test and have a Type 2 error and fail to reject the Ho when you should have.
Levene’s test is a common test used to determine if your sample groups have equal variances. Bartlett’s test is also used frequently to test for homogeneity of variance. The Levene test is more robust than Barlett for nonnormality. Therefore, if you have evidence that your sample data comes from an approximately normal distribution, then Bartlett is a more powerful test.
3 benefits of homogeneity of variance
Your hypothesis tests and regression analyses are enhanced by meeting the assumption of homogeneity of variance.
1. Validates the conclusions of various statistical tests
The conclusions of your t-tests, ANOVA and regression analysis will be valid if you meet the test assumptions including homogeneity of variance.
2. Avoids problems with Type 1 errors
By not meeting the assumption of homogeneity of variance, you may increase the probability of over or underestimating the significance and power of your test which may result in making a Type 1 or 2 error.
3. Somewhat robust to violation
Your assumption of homogeneity of variance may be robust to violation if your sample sizes are large enough and not too dissimilar in size.
Why is homogeneity important to understand?
Ignoring or not properly testing for homogeneity of variance may lead to erroneous conclusions about your data.
Pooled estimate of variance
Some of the calculations in your hypothesis testing and regression use a pooled variance or standard deviation which assumes you’re pooling variances of approximately equal size.
Assures distribution of your groups are essentially equal
Equal variance will help give you assurance that the distributions of your samples and populations are essentially equal.
Provides insight into possible Type 1 or 2 errors
If you fail the test for equal variance, you will have some insight into whether you should be concerned about making a Type 1 or 2 error.
An industry example of homogeneity of variance
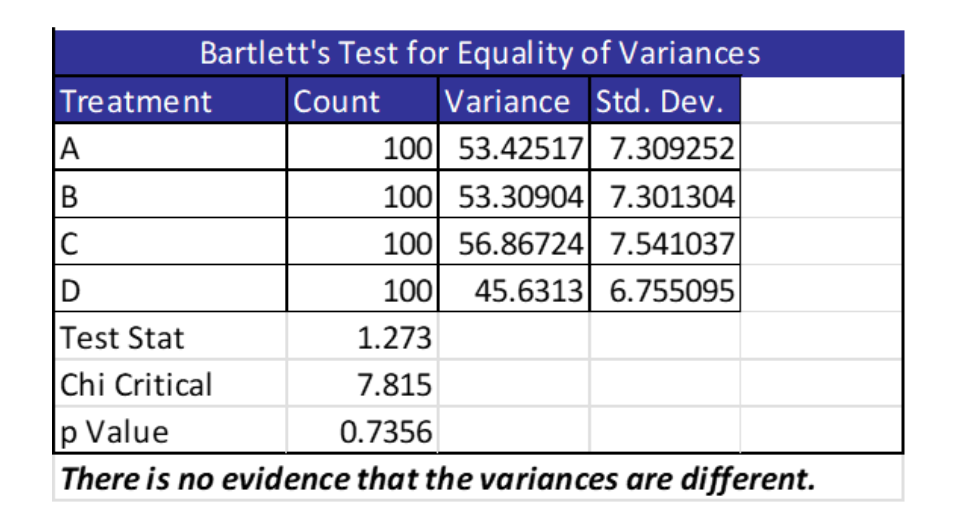
The HR Manager was reviewing turnover statistics and wanted to know if there was any statistical difference in turnover across the company’s four sites. She was advised to use ANOVA to determine if the average turnover is different. She decided to first test the assumption of homogeneity of variance. Below are the results from the statistical software she used.
Because the p-value is greater than their selected alpha risk of .05, the manager concluded the four variances are statistically equal.
3 best practices when thinking about homogeneity of variance
Here are a few tips to help you understand how to handle homogeneity of variance.
1. Test for homogeneity of variance before testing your means
Often, it is best to test for all assumptions before going ahead and doing your desired statistical test. The common ones are testing the assumption of normality and homogeneity of variance.
2. Try to obtain group samples of approximately the same size
Varying sample sizes may impact your variance and thus the homogeneity of those group variances.
3. Consider using Welch’s test or nonparametric test.
If you fail your initial assumptions of equal variance, you can use Welch’s test where appropriate or a nonparametric test or as a last resort, transform your data.
Frequently Asked Questions (FAQ) about homogeneity of variance
What if my data groups don’t have equal variances?
If you are doing a 2-sample t test you can use Welch’s test which does not have an assumption of equal variance.
How do I interpret the Levene’s test?
The null hypothesis is that the variances are equal. The alternative hypothesis is they are different. If your p-value is smaller than your alpha risk, you will reject the null hypothesis and conclude your variances are not equal.
If my data is not normally distributed, which test should I use for homogeneity of variance?
The Levene test is more robust to violations of the normality assumption.
Wrapping up homogeneity of variance
Several statistical tools have an underlying assumption of equal variance or homogeneity of variance. If the assumption is violated, your results may not be valid. There are a variety of options and alternatives which you can use to get the answers you want despite not being compliant with the assumption of equal variance.