Most parametric hypothesis tests have an underlying assumption that the data follows a specific distribution, typically the normal distribution. If your data is normal, you can now use the mean of two or more samples to see if they come from different populations. If not, you might have to use the Mood’s Median non-parametric test. As a non-parametric test, there is no underlying assumption for the distribution of the data.
Overview: What is the Mood’s Median Test?
The Mood’s Median Test tests the null hypothesis that there is no difference in the medians of the populations from which the samples came from. The alternative hypothesis states there is a difference in the mediums of the populations which the samples came from.
Once the median of the combined data is determined, the sample values are put into one of two groups, one which has all the values above the median and the other all values at the median or below. A chi square test is used to compare the actual frequencies of these two groups against those which would be expected should there be no differences. The p-value of the test indicates whether you should or should not reject the null hypothesis.
While the Mood’s Median test does not make any assumptions about the distribution of the data, there are still other assumptions that should be met. They are:
- The sample values are independent both within and between samples
- The sample values come from populations with a continuous rather than discrete distribution
- The distributions of the populations the samples were drawn from all have the same shape
An industry example of the Mood’s Median Test
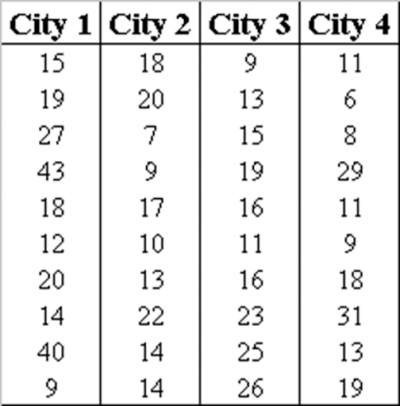
The sales manager of a large consumer products company was curious whether there was any statistically significant difference in sales volume between the 4 cities he manages. His Six Sigma Master Black Belt (MBB) suggested he try using ANOVA if his sales data was normally distributed. Unfortunately, it wasn’t so the MBB recommended he use a Mood’s Median Test.
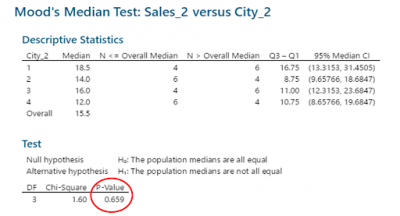
Below is the data set that was being analyzed as well as the output of the test. According to the p-value there is no statistical difference in the medians of the 4 cities despite what intuition might tell you.
Frequently Asked Questions (FAQ) about the Mood’s Median Test
What is the equivalent parametric test for the Mood’s Median Test?
Analysis of Variance (ANOVA) tests for the difference in means between two or more samples. If the underlying assumptions, including the normality of each sample data set, are met then ANOVA can be used. If not, the Mood’s Median could be used.
What is the difference between the Mood’s Median Test and the Kruskal-Wallis test?
The Kruskal-Wallis test is also a nonparametric test for comparing two or more sample medians. The Kruskal-Wallis test is more powerful than the Mood’s Median test for data from many distributions, including data from the normal distribution, but it is less robust against outliers.
What is the Mood’s Median Test used for?
The Mood’s Median Test is used for determining whether the medians of two or more sample data sets come from the same population or not.