Key Points

• The Wilcoxon Rank Sum Test is a non-parametric means of comparing data between two sets.
• It operates as a useful alternative to the 2-sample t-test.

The Wilcoxon Rank Sum Test sometimes called the Mann Whitney Wilcoxon Test or Mann Whitney U test, is used to test whether two independent samples come from the same population or two different populations. 

Since the Wilcoxon Rank Sum Test is a form of hypothesis testing, there will be an associated null and alternative hypothesis. The test is used for continuous data. Let’s learn a little more about the Wilcoxon Rank Sum Test.

Overview

The test is named for Frank Wilcoxon (1892–1965) who was a chemist and statistician. The Wilcoxon Rank Sum Test is often described as the non-parametric version of the 2-sample t-test. Recall that the 2-sample t-test is used for comparing two population means. The underlying assumptions of the 2-sample t-test are that:

1. The two samples are independent of each other
2. The two populations have equal variance
3. The two populations are normally distributed

The first assumption must be satisfied for a 2-sample t-test. When the assumptions of equal variance and normality are not satisfied, but the samples are large, you can say the assumptions are robust and your results are approximately correct. But when your samples are small and your data is skewed or non-normal, you should consider a Plan B.

The Wilcoxon Rank Sum Test is your Plan B. It only requires the first two assumptions of independence and equal variance. It does not assume your data has a known distribution. Since the Wilcoxon Rank Sum Test does not assume a known distribution, it does not deal with parameters, and therefore it is called a non-parametric test.

Whereas the null hypothesis of the 2-sample t-test is equal population means, the null hypothesis of the Wilcoxon tests for equal population medians. If you reject the null, that means you have evidence that the two population medians from where the samples were taken are different. The Wilcoxon test, and its variations, can be used as a 1-sample, 2-sample (independent), or 2-sample (paired) test.

Why It Matters

You’re likely already used to running t-tests for two normally distributed sets of data. However, data is rarely uniform, nor does it conform to normality. As such, having the means to handle data that doesn’t fit within those parameters is paramount. The Wilcoxon Rank Sum Test is a flexible non-parametric means of evaluating two disparate sources of data.

An Industry Example

The production manager was trying to compare the performance of two sites. He randomly collected two sets of independent data. His Master Black Belt suggested he use a 2-sample t-test if the assumptions are met. Unfortunately, as you can see below, neither of the data sets were normally distributed.

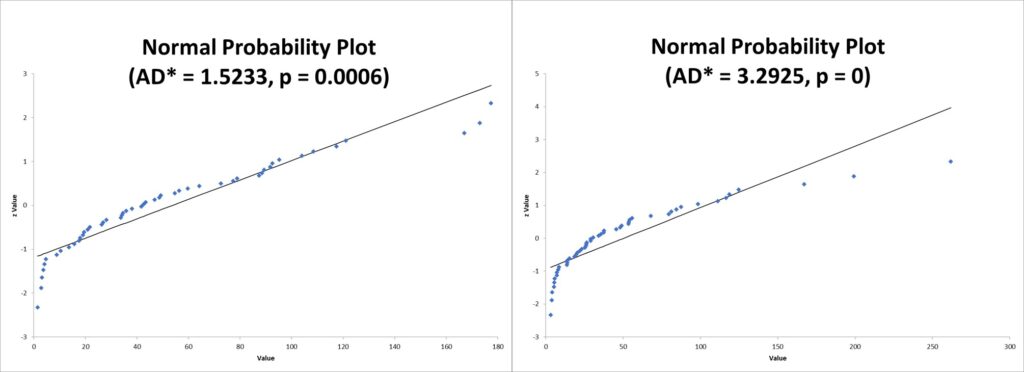
It was then suggested he try using a Wilcoxon Rank Sum Test. The assumption of equal variances was tested, and the graphic below shows the two groups of data have equal variances.

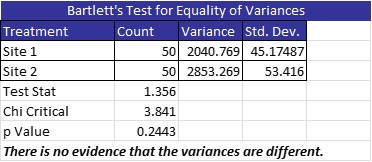
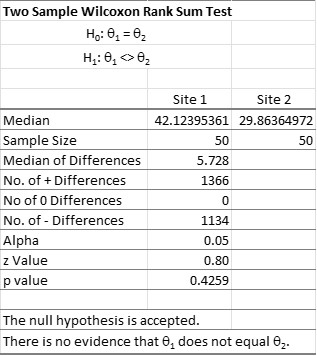
Now that the assumptions have been fulfilled, the manager ran the Wilcoxon Rank Sum Test. As you can see, there was no difference between the two sites.

Other Useful Tools and Concepts

Looking for some more useful tools in your Six Sigma toolbox? Why not take a closer look at Cpk? This handy calculation is a great way to gain insight into your production workflow. It is one of the cornerstones of the Six Sigma methodology and also can be readily converted to other measurements.

Additionally, learning how to account for variation in your processes is a great way of managing defects and waste. Red X is a complementary approach to the typical DMAIC, automatically assuming that any production is going to have variation.