This two-part article explores the concept of uncertainty quantification (UQ). In Part 1, we will learn the basics of UQ and how UQ works with Six Sigma. Part 2 presents a case study looking at UQ in action.
The Six Sigma methodology includes proven tools, primarily founded in collecting and analyzing physical data using statistical means. Continual increases in computational power coupled with advances in simulation accuracy, however, have made simulation modeling a feasible method for analytics that can enhance Six Sigma methodologies. For example, augmenting the Six Sigma process with computer simulations can reduce expensive and time-consuming physical test requirements. In addition, Six Sigma practitioners can explore a wider variety of solution options in the simulation environment more quickly and at lower cost than traditional physical test methods.
While the prevalence of simulation tools offers unique potential to generate expedient analytics, it does so through uncertainty quantification (UQ) – advanced statistical techniques that, when applied to simulations of complex systems, generate actionable results. UQ is the next generation of analytical tools that brings further insights into reducing process variability.
Six Sigma Challenges
Listed below are some of the common problems Six Sigma Black Belts and engineers face while implementing Six Sigma techniques:
- Ensuring that the quality and quantity of data collected are sufficient for making decisions
- Designing a new process or product when there is no baseline data to collect
- Analyzing complex processes can be time-consuming when using traditional statistical methods
- Justifying the high cost of physical testing
- Quantifying the improvements in a process with only a small number of physical tests
- Conducting physical design of experiment (DOE) tests in an environment where they are impractical
What Is Uncertainty Quantification?
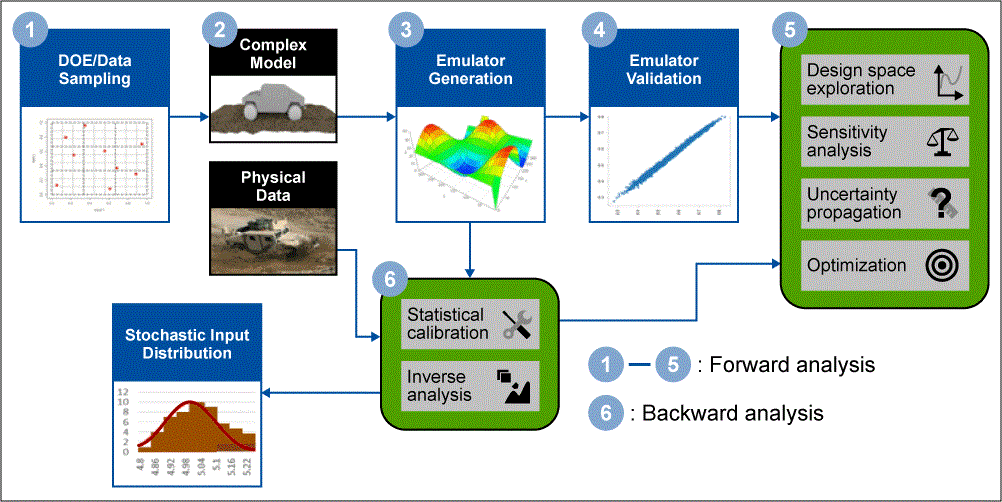
According to definitions from the National Agency for Finite Element Methods and Standards (NAFEMS) Stochastics Working Group and the American Society of Mechanical Engineers (ASME) Standards Committee on Verification and Validation, uncertainty quantification is the formulation of a statistical model to characterize imperfect and/or unknown information in engineering simulation and physical testing for predictions and decision-making. UQ seeks to address the problems associated with incorporating real-world variability and probabilistic behaviors into engineering and systems analysis. The figure below shows the workflow for UQ.
1-2: DOEs: DOEs are systematic sampling patterns used to conduct experiments to determine cause-and-effect relationships between inputs and outputs. Using a DOE saves time over random sampling methods through the judicious selection of sample points that maximize the information sought with a minimum number of simulation runs or experiments. Moreover, space-filling DOEs (e.g., Latin hypercube design) are especially efficient for exploring the solution space when using computer simulations.
3-4: Emulators: Emulators are advanced statistical models built to mimic the physics-based simulation. They are also known as surrogates or metamodels. Emulators reduce the computational burden of the physics-based simulation since they are designed to run in a fraction of the time required for the simulation. In doing so, they become the analytical workhorse for propagating uncertainty, exploring the design space, performing optimization and discovering inverse solutions. Some of today’s emulators are built using machine-learning algorithms, which enable fast-fitting times and greater accuracy especially when replicating large systems.
5: Sensitivity Analysis: Sensitivity analysis is a process that is applied to both simulation and physical test methods. It quantifies the variation in the analytical results with respect to changes in the analytical inputs. Sensitivity analysis answers several important questions:
- Which inputs have the greatest influence on results critical to quality?
- Which geometric parameters should have tighter manufacturing tolerances to ensure process improvements are met, and which parameters can have relaxed tolerances?
- Is there evidence of interactions among the inputs that need to be investigated?
5: Propagation of Uncertainty: The propagation of uncertainty tells the analyst how robust a design is to process by calculating the effects of input uncertainties on the simulation outputs. Uncertainty propagation answers the question: How robust are my solutions to variations that will likely occur in manufacturing? This is especially useful when wanting to know how likely is it that the process improvement goals will be achieved.
5: Optimization: Optimization finds values of design variables that optimize design performance. Emulator-based optimization is the application of optimization algorithms to an emulator, taking advantage of the extremely fast prediction speeds to exhaustively cover the design space. Studies conducted have shown that it is best to include UQ as part of the optimization analysis instead of quantifying uncertainties only after locating the optimum.
6: Calibration: Calibration is a process that “tunes” the model to improve its ability to replicate reality. The process uses measured data from a physical system as input into the simulation model representing the physical system. Certain simulation model input parameters (e.g., calibration parameters) that are not directly measured in the physical system are adjusted to improve the model’s ability to agree with the physical data.
Statistical calibration goes further and quantifies uncertainties that come from the simulation model and input parameters. Why is this important? Not all calibration processes account for these sources of uncertainties. A discrepancy function is generated from the differences between the simulation and the physical data which, when applied to the simulation, can make the model’s predictions more realistic. Statistical calibration is a better option to use when calibrating the model because it accounts for these uncertainties that are typically unknown and can be significant.
6: Inverse Analysis: Inverse analysis improves the model’s predictive capability by generating a better understanding of an unknown stochastic model input parameter. In the context of the process shown in the figure above, inverse analysis is used to estimate the underlying distribution for model inputs that are unknown because of missing data or data that is poorly characterized and noisy. Representing the unknown stochastic model input with a distribution reduces the uncertainty in the model outputs when used to make predictions. Inverse analysis answers the question: How can I reduce process variation when I have noisy or missing input data?
Comparison of Six Sigma and UQ
Six Sigma: Six Sigma is a quantitative, mathematical approach for making cultural changes to an organization. It is a data-driven approach that uses statistical models and probability to reduce process variations. Six Sigma primarily employs statistical methods like general linear regression models, statistical tests, probability distributions, DOEs and analysis of variance (ANOVA). The value of reducing process variations is in reducing the risk of delivering poor quality products – making customers pleased with their choice of purchase.
UQ: Conversely, UQ is a multi-disciplinary field that brings together modern statistics, applied mathematics and computer science methods to quantify uncertainties in engineering analytics, where computer simulations are often the analytical method of choice. UQ is a probabilistic approach that can be described as a deterministic approach that is systematically repeated. It uses the inputs and responses from the multiple simulation runs to build a predictive statistical model. Once validated, the statistical model or emulator is then used in place of the original simulation as the analytical workhorse since it runs in a fraction of the time needed for the original simulation. The objective of UQ’s probabilistic approach is to determine how likely are certain outcomes if some aspects of the complex system are not exactly known.
Knowing the level of uncertainties from a simulation is important for two reasons:
- The uncertainty can be propagated through the emulator to forecast the range of possible outcomes and the most likely solution well before committing valuable resources on a project. If the results are not within an acceptable range, then the UQ process provides the analyst the next steps to take to make it acceptable.
- The second reason involves the risks when making critical decisions. The quantified uncertainty represents the probability of an event occurring while risk is the consequence when the event occurs. Decision makers are better informed of the risks involved when uncertainties are quantified in the analysis. The result of acknowledging uncertainties in the analysis as part of the decision process typically yields more favorable outcomes from those decisions.
Both Six Sigma and UQ use statistical models to solve problems but they are solving different problems for different reasons. Six Sigma seeks to identify and eliminate defects and to minimize variability in a process. UQ seeks to quantify what is unknown about a given analysis to determine ways to reduce it. In addition, UQ is used to better inform decision makers of the risks involved when making critical technical or programmatic decisions.
Industrial ROI of UQ
UQ enables a one-time process for product development: The biggest bang for the buck for UQ can be found in product development. Variability can be viewed as a cost driver when designing or analyzing a new model or system. The probabilistic approach used with UQ reduces these process iterations that can happen during the design or analysis phases. Additional cost reductions are realized when each design iteration includes procuring and testing prototypes. Essentially, UQ enables the ability to have a one-time process for product development.
Maximize product reliability and durability: Using UQ techniques can be used in a quality campaign to reduce part-to-part variability and increase product life. This can be accomplished in the design phase by conducting sensitivity analysis to first identify which model parameters have the greatest influence on the variation. The next step would be conducting an optimization with emphasis on varying these identified parameters to find an optimum that improves the reliability/durability performance. Understanding the robustness of the optimum can be assessed by propagating uncertainties through the model.
Ensure simulation results are credible and realistic: When using the deterministic approach, sometimes extreme values of load and material strength are used in a finite element analysis of a component instead of expected values. The assumption in this approach is if the results are favorable in meeting target lifetime goals, then it will likely survive under the expected conditions. However, the extreme value approach is not necessarily credible or realistic, which affects how trustworthy can the model be when using it to make predictions. Using UQ in a probabilistic approach, which relies on the simulation results to be credible and realistic, generates a trustworthy (e.g., model validation) and that is essential for understanding the risks when using simulation results in the decision-making process.
Government oversight: The benefits of modeling and simulation have been recognized at a policy level by several federal agencies (such as the FAA, DOD and FDA) of the U.S. government. Agencies are evaluating methods to verify and validate computer models such that the simulation results are trustworthy sources of information capable of meeting stringent federal regulations. The basis of validation methods is UQ.
How UQ Can Enhance Six Sigma with Simulation
Increases in computational power and computer simulation accuracy have made simulation modeling an efficient method for analyzing complex engineering systems. UQ methods essentially put “error bars” on simulations, making the results trustworthy and credible.
Simulations that use UQ methods have many advantages, including:
- Providing accurate analytics on a process or system when physical testing is impractical
- Identifying parameters that govern the variations in manufacturing
- Efficiently exploring the design space in less time and at lower cost than testing methods
- Generating baseline data for a new product or process
Using simulations complement the analytical capabilities of Six Sigma. And coupling UQ with simulations results in significant acceleration of the analytical process. The additional analytical information provided comes from the synergism of combining simulation and physical data. And that information can help decision makers choose more wisely.
Simulations can be used in a Six Sigma framework when physical data is impractical to acquire or to generate baseline data when there is no data to collect. They can also be used to efficiently explore the design space in less time and at a lower cost than test methods. UQ provides valuable information to augment the decision-making process. Knowing the uncertainty and the consequences leads to making decisions with more favorable outcomes.
Click here for Part 2 – a UQ case study.
Image courtesy of SmartUQ.