
One of the pleasures of teaching Green Belts is helping to eliminate the fear of statistical analysis. One technique is to place an emphasis on not only when and why a tool or methodology is used but also what the data says in “plain English.” Memorizing complex formulas may be the goal of many Master Black Belts; however, a Green Belt typically does not need such an in-depth span of knowledge. Basic formulas, however, should be shared.
Here is an example. Determining the average, or mean, of a sample or population is not complicated statistics. Given the following data set:
| Table 1: Data Set | ||||
| 2.58 | 2.19 | 0.70 | 2.19 | 2.03 |
| 4.10 | 3.42 | 1.72 | 1.62 | 1.32 |
| 2.28 | 1.61 | 2.27 | 1.45 | 2.26 |
| 2.51 | 1.42 | 1.33 | 3.68 | 3.52 |
| 1.81 | 1.42 | 2.43 | 1.74 | 2.25 |
One simply adds up all of the numbers in each data set and divides by the total quantity of numbers in their respective data set. In this case, the total is 53.85 divided by the total quantity, 25. The average is 2.154. The formula for average is represented as:
∑ ![]()
At first glance, a novice math student would not easily recognize this formula as representing the average. Eliminate the fear!
The same holds true in determining confidence intervals. One way is to provide examples to explain the central limit theorem. The primary point of a classroom module was to show that as additional samples are drawn, data tends to approach a normal distribution. During class examples, estimates can be made from a single sample of data drawn from a larger population. Theoretically, if yet another sample was to be drawn from the same population, it would be likely that the estimates of the variance, standard deviation and mean would be different, and none would be have the exact value of the population parameter. This fact can turn the discussion to the use of confidence intervals.
In order to compensate for variation in sampling, use confidence intervals. These intervals contain the true – but unknown – population parameter for the percentage of the time chosen by the Green Belt. As a basic example, if the Green Belt were to calculate 95 percent confidence intervals for the mean, 95 percent of the intervals calculated from samples drawn from the population would contain the true population mean while 5 percent would not.
Determining Confidence Intervals Representing the Mean (Continuous Data)
Keeping with the spirit of eliminating the fear of formulas, here is a simple confidence interval formula. If the distribution is normal or the population standard deviation is known for a large sample size, one can use the normal distribution to calculate the confidence interval for the mean.
The formula is:
![]()
Where:
XBar = the point estimate of the average
![]() = the population standard deviation
= the population standard deviation
![]() = the normal distribution value for a given confidence level (can be obtained from the Z table for a normal distribution).
= the normal distribution value for a given confidence level (can be obtained from the Z table for a normal distribution).
Example: Calculate the 95 percent confidence interval for the average if the sample size is 25.
Known Data: 2.15 is the estimate of the average (taken from the table above); .8 is the population standard deviation
Referencing the Z table above, the value for ![]() would be 95/2 or .475. The Z value is then 1.96. The 95 percent confidence interval would be calculated as:
would be 95/2 or .475. The Z value is then 1.96. The 95 percent confidence interval would be calculated as:
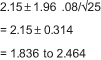
In “plain English,” with a 95 percent degree of confidence and based on the current sample size, the range can be expected to be between 1.836 and 2.464.
If the sample standard deviation is estimated from a small (operational definition of small in this case is fewer than 50) sample as in the 25 data points in the above example, the formula becomes:
![]()
Where: ![]() = value found in Table B for (n-1) degrees of freedom. (Table B is an adaptation of Table III from Statistical Tables for Biological, Agricultural and Medical Research by Fisher and Yates.)
= value found in Table B for (n-1) degrees of freedom. (Table B is an adaptation of Table III from Statistical Tables for Biological, Agricultural and Medical Research by Fisher and Yates.)
Where: s = the estimate of the population standard deviation from the sample data
Example: The data used above provided an estimate of the mean (XBar) of 2.15 and a standard deviation estimate of .82. In order to calculate the 95 percent confidence interval for the mean, the formula translates as follows:

Other Calculations of Confidence Intervals
The example above relates to calculating the confidence interval for the mean of continuous data. This explanation may result in a deer-in-the-headlights look from students. Keep in mind, there are many other examples available with more complex formulas. For example:
- Confidence interval for fraction nonconforming – normal distribution
- Confidence interval for the variance
- Confidence interval for proportion
- Confidence interval for poisson distributed data
These items do no need to be discussed in depth a Green Belt class. Students who majored in statistics might enjoy the example, but the rest of the class might be lost.
Eliminating the Fear
It is not necessary to have a Ph.D. in statistical analysis to convey the true meaning of confidence intervals. Simply stated, the confidence interval is the range where one expects something to be. By saying “expect,” this leaves open the possibility of being wrong. The degree of confidence measures the probability of that expectation to be true.
The degree of confidence is linked with the width of the confidence interval. It is easy to be very confident that something will be within a very wide range, and vice versa. Also, the amount of information (typically related with the sample size) has an influence on the degree of confidence and the width of the confidence interval. With more information, one can be more confident that “the thing” will be within a given interval. Also, with more information, and keeping a given degree of confidence, the interval can be narrowed.
Here is a good example to finish with:
In a certain bar, a survey is made. The question is: “Do you prefer Beefeater gin or Tanqueray gin?” Sixty percent answer Beefeater, and 40 percent answer Tanqueray. So an estimation is that in this bar, 60 percent prefer Beefeater. Does it mean that 60 percent of the population of bars in this area prefer Beefeater? No, unless the survey had been answered by all the population. However, one can be somehow “confident” that the actual proportion of people choosing Beefeater will be within some interval around the 60 percent found in the sample. How confident? How wide is the interval?
If the survey is based on a sample of 100 patrons, one can be 90 percent confident that the actual proportion of Beefeater drinkers will be between 52 percent and 68 percent. Also, one can be 99 percent confident that the actual proportion will be between 48 percent and 72 percent (for the same sample size, there is more confidence because of the wider interval).
If the survey had been on a sample of 1,000 patrons instead of 100, one could be 90 percent confident that the actual proportion is between 57.5 percent and 62.5 percent (compared with 52 percent and 68 percent for the same confidence with a sample of 100; a larger sample and narrower interval for the same degree of confidence). In addition, one could be 99.99998 percent (say 100 percent?) confident that the actual proportion will be between 52 percent and 68 percent (compared with a degree of confidence of 90 percent for the same interval with a sample of 100; in this case, the larger sample gives a better degree of confidence for the same interval).
All of this was discussed without a single formula. Other items to use in an example are soft drinks or food.