
As with all probability distributions, the Normal Distribution describes how the values of your data are distributed. It is one of the most important probability distributions in statistics because it accurately describes the distribution of values for many natural phenomena.
Overview: What is the Normal Distribution?
The Normal Distribution, also known as the Gaussian Distribution, is a hypothetical mathematical construct and one of the most common statistical distributions. In 1809, Johann Carl Friedrich Gauss, a German mathematician and physicist described the distribution in the context of measurement errors in astronomy. During the 19th century, this distribution was widely applied in the areas of applied probability and statistics.
Since the Normal Distribution is a hypothetical curve there is no such thing as a Normal Distribution in the real world. The key is how close it can be used to describe and estimate your actual data. The following are the characteristics of the Normal Distribution:

The formula for the Normal Distribution probability density function is shown below. Note that the only variable parameters are the mean and standard deviation.
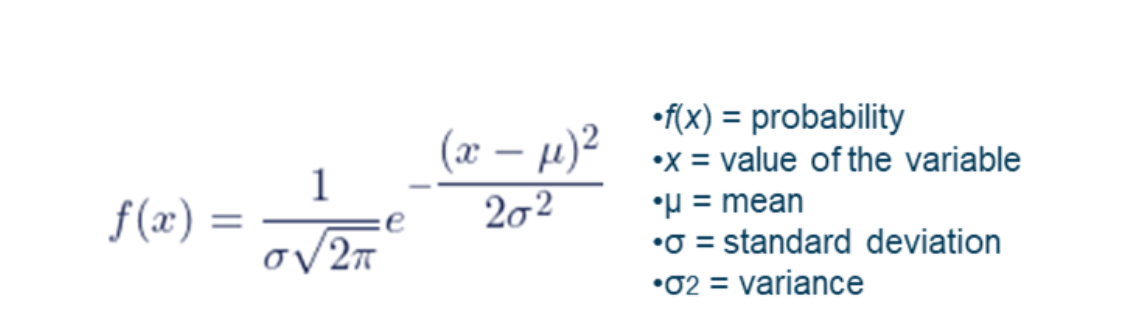
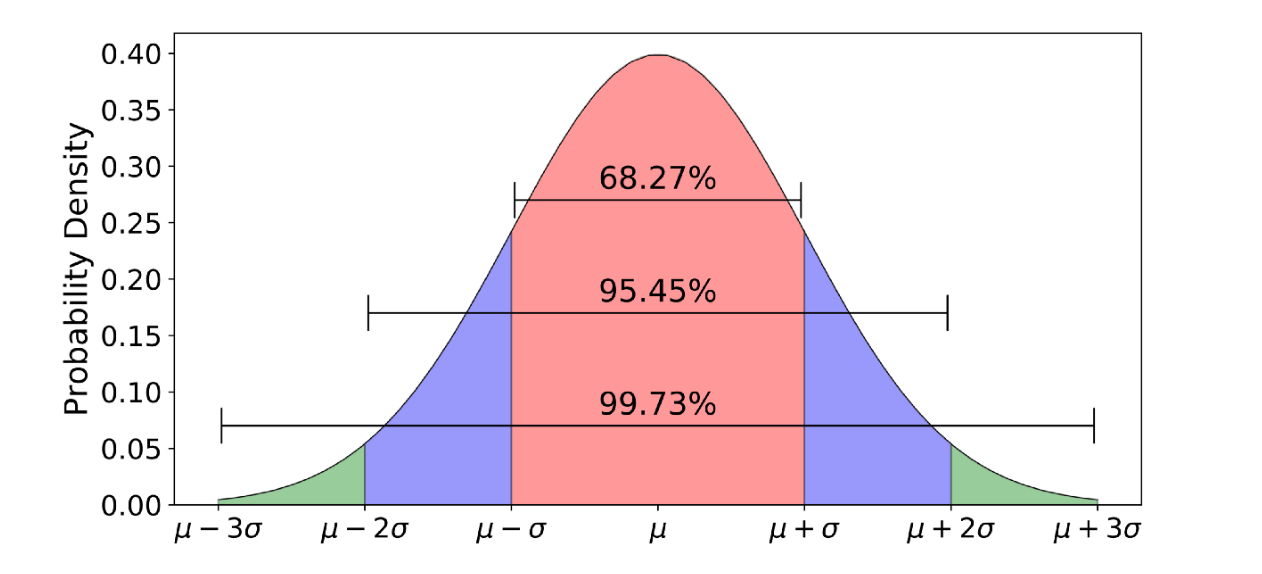
The Empirical Rule describes how the individual values of your data would be distributed under the distribution curve if your data was normally distributed. It will be based upon the mean and standard deviation of your data. This is shown below.
If your data is not approximately distributed as the above, you may not want to declare your data is normal. You can use a graphical Probability Plot or a statistical test like the Anderson-Darling test and use the p-value to test whether your data is non-normal.
3 benefits of the Normal Distribution
As one of the most common statistical distributions, there are a number of benefits of the Normal Distribution.
1. Describes many processes
The Normal Distribution can be used to model many common processes and as such, is the underlying assumption for the use of many statistical tools.
2. Existence of tables
As a result of being such a common distribution, statisticians have developed a number of Normal and Standard Normal Distribution tables which can be used for calculations and predictions.
3. Link to the Central Limit Theorem
A major benefit of the normal distribution is the linkage to the Central Limit Theorem. This theorem states that when the sample size is sufficiently large, the distribution of sample means will approach a normal distribution regardless of the shape of the distribution from which the samples came from. This allows you to use inferential statistical methods that assume normality, even if the individual data in your sample doesn’t follow a Normal Distribution.
Why is the Normal Distribution important to understand?
As the most common distribution, it is important to understand what the Normal Distribution is and how to properly use it.
Assumption of many statistical tests
There are many statistical tests which have an assumption that your data should be normally distributed for the test to be valid. This frequently occurs in hypothesis testing.
Represents many natural phenomenon
Many natural processes can be described using the Normal Distribution.
Computations are not complex
The Normal Distribution is described by only two parameters, the mean and standard deviation making calculations easy to do.
An industry example of the Normal Distribution
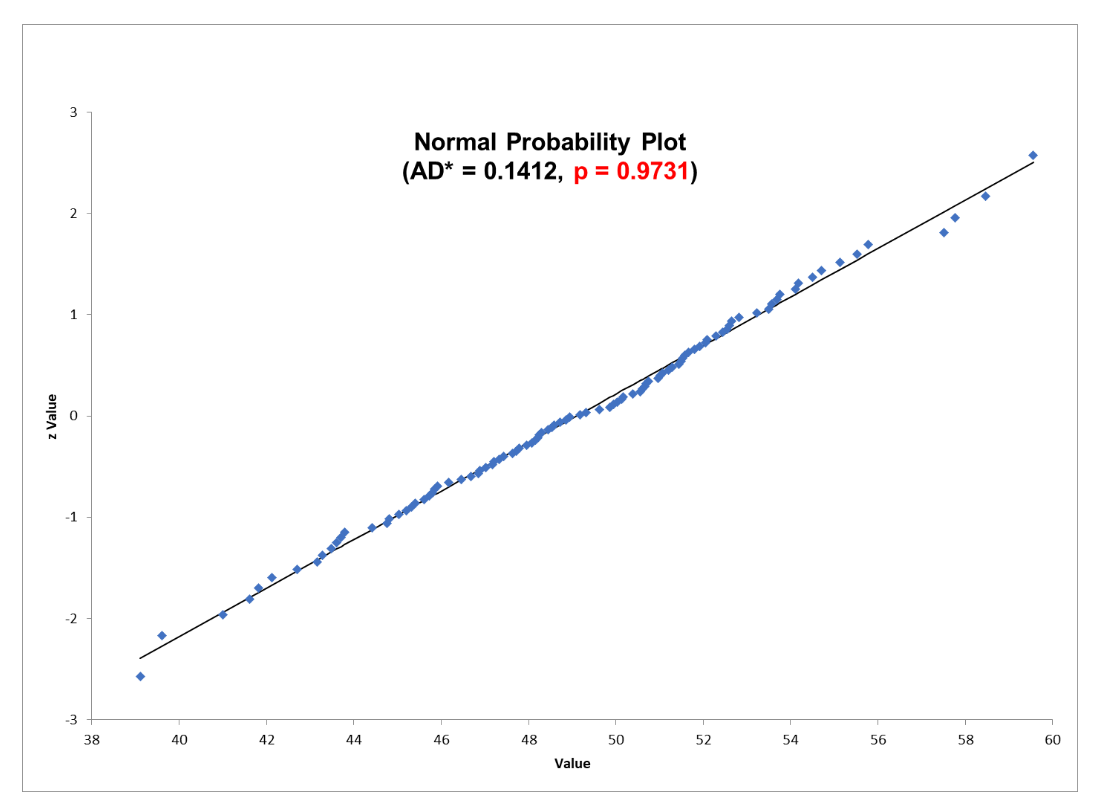
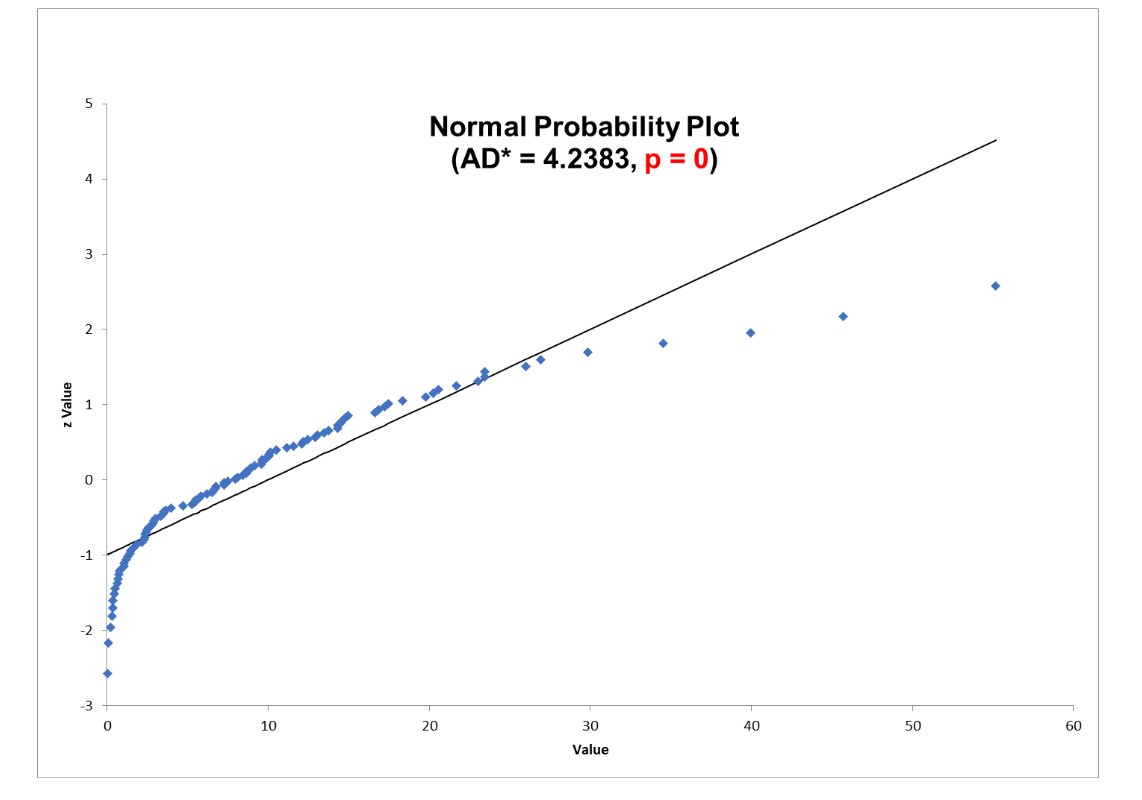
A Six Sigma Green Belt wanted to know whether his data fulfilled the assumption of normality as required by the 2-sample t-test he wanted to do. Below are two probability plots for his two sets of data. Notice that one can be considered normal while the other is not. If the p-value is greater than .05 you can claim the data is not different than normal. If less than .05, you will reject the null hypothesis and conclude the data is not normal.
3 best practices when thinking about the Normal Distribution
Despite its simplicity, there are some things to keep in mind when using the Normal Distribution to describe your process data.
1. Be sure you have enough data
The Normal Distribution is only a good predictor if you have an adequate amount of data. It takes a sufficient amount of data for the distribution to form.
2. Be sure your data is continuous
The Normal Distribution is a continuous distribution so it is only valid for continuous data. In some cases, you can use the Normal Distribution to approximate discrete distributions such as the Binomial and Poisson.
3. Test your data for normality
There are some simple statistical as well as graphical methods for testing the normality of a set of data. The Normal Probability Plot and the Anderson-Darling Test can be used as a graphical and statistical tool for assessing non normality. But, keep in mind, there are statistical tools which are robust and forgiving if there is a lack of normality.
Frequently Asked Questions (FAQ) about the Normal Distribution
What statistical parameters define the Normal Distribution?
The population parameters which define the Normal Distribution are the mean and standard deviation.
What is the empirical rule?
The empirical rule defines how the values are distributed in a Normal Distribution. If a distribution is normal, you would expect your values to be distributed with approximately:
- 68.27% of the values contained within the mean plus and minus 1 standard deviation
- 95.45% of the values contained within the mean plus and minus 2 standard deviations
- 99.73% of the values contained within the mean plus and minus 3 standard deviations
What is the difference between the Normal and Standard Normal Distribution?
The Normal Distribution is represented by your actual values. The Standard Normal Distribution is a form of Normal Distribution where the mean is 0 and the standard deviation is 1.
Wrapping up the Normal Distribution
The Normal Distribution is a continuous probability distribution defined by the mean and standard. It is one of the most common distributions because it describes many natural phenomena. As a result, it is the underlying assumption of many statistical tools.
The Empirical Rule helps describe how your data values are distributed under the distribution curve. Statistical and graphical tools can be used to confirm whether your data approximates a Normal Distribution.